앞에서 봤던 트리의 종류 중 높이가 h이고 노드수가 n개 일 때, 포화 이진트리의 1번부터 n번까지 빈자리가 없는 트리였던 완전 이진 트리에 있는 노드 중 키 값이 가장 큰 노드 or 키 값이 가장 작은 노드를 찾기 위해 만든 자료 구조이다.
최대 힙 (max heap)
- 키 값이 가장 큰 노드를 찾기 위한 완전 이진트리
- (부모 노드의 키값 > 자식 노드의 키값)
- 루트 노드 : 키값이 가장 큰 노드
최소 힙 (min heap)
- 키 값이 가장 작은 노드를 찾기 위한 완전 이진트리
- (부모 노드의 키 값 < 자식 노드의 키 값)
- 루트 노드 : 키값이 가장 작은 노드

삽입


삭제
- 힙에서는 루트 노드만이 삭제 가능
- 루트 노드의 원소를 삭제하여 반환
- 힙의 종류에 따라 최솟값 또는 최댓값 구하기 가능

# 파이썬에서의 힙(heap)
- 힙의 키를 우선순위로 활용하여 우선순위 큐를 구현할 수 있다.
2022.09.09 - [CS/자료구조] - [자료구조] 큐(Queue) - 선형 큐, 원형 큐, 우선순위 큐
[자료구조] 큐(Queue) - 선형 큐, 원형 큐, 우선순위 큐
이전에 배웠던 스택과 마찬가지로 삽입과 삭제의 위치가 제한적인 자료구조이다. 동적 자료형인 리스트 자료형을 사용한다 선입선출 구조(FIFO : First In First Out) 큐의 뒤에서는 삽입만 하고, 큐
cheon2308.tistory.com
앞의 글에서는 heap에 대해 알지 못하여 기본 동작에 대해 이론으로 알아보았다.
최대 힙, 최소 힙의 루트 노드들은 우선순위를 항상 가지며 이를 활용한다.
이때, 키 값의 대소 관계는 부모/자식 간에만 성립, 형제 노드 사이에는 대소 관계가 정해지지 않는다.
heapq 모듈
- 파이썬에서 제공하는 heapq 내장 모듈이다.
- 모든 부모 노드는 그의 자식 노드보다 값이 작거나 큰 완전 이진트리 구조
- 내부적으로는 인덱스 0에서 시작해 k번째 원소가 항상 자식 원소들(2k+1, 2k+2) 보다 작거나 같은 최소 힙의 형태로 정렬
# 활용
- heapq.heappush(heap, item) : item을 heap에 추가
- heapq.heappop(heap) : heap에서 가장 작은 원소를 pop 한 후 return. -> 비어 있는 경우 indexError
- heapq.heapify(x) : 리스트 x를 즉각적으로 heap으로 변환함 (in linear time, O(N))
heapq모듈은 최소 힙만을 지원하기 때문에 최대 힙을 만들기 위해서는 몇 가지 작업이 필요하다.
다른 분의 코드를 참조해보면 heap에 원소를 추가할 때 (-item, item)의 튜플 형태로 넣어준다면 첫 번째 원소를 우선순위로 힙을 구성한다.
이때, 원소 값의 부호를 바꿨기 때문에 최대 힙을 구현할 수 있다.
heap_items = [1,3,5,7,9]
max_heap = []
for item in heap_items:
heapq.heappush(max_heap, (-item, item))
print(max_heap)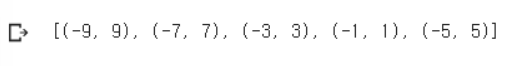
이후 heappop을 사용하며 [1] 번 인덱스를 반환해준다면 최댓값이 반환된다.
max_item = heapq.heappop(max_heap)[1]
print(max_item)
참고 : https://littlefoxdiary.tistory.com/3
heapq vs PriorityQueue
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] Fenwick Tree(Binary Indexed Tree, BIT) with Python (0) | 2022.11.30 |
|---|---|
| [자료구조] 그래프 with Python (0) | 2022.09.28 |
| [자료구조] 트리 2 - 이진 탐색 트리 with Python (0) | 2022.09.15 |
| [자료구조] 트리 (Tree) 1 with Python (1) | 2022.09.13 |
| [자료구조] 해시(hash) with Python (0) | 2022.09.09 |
