해시 구조를 이해하기 위해서 먼저 해시 테이블에 대해 알아보자.
1. 해시 테이블?
- 연관 배열 구조를 이용하여 키(key)와 결과 값(value)를 저장하는 자료구조
- 연관 배열 구조란 - key와 value가 1:1로 연관 되어 있는 구조이다.
- 파이썬의 Dictionary!
- 지원하는 명령
- key와 value 저장
- key가 주어질 때, 연관 value를 얻는 명령
- key와 value가 주어질 때, 원래 key의 value값 수정
- key가 주어질 때, 연관 value 제거\
- 구조

해시 테이블의 경우 키(Key), 해시 함수(Hash Function), 해시(Hash), 값(value), 저장소(Bucket, Slot)로 이루어져 있다.
위 그림에서 볼 수 있듯이 키(key)는 해시함수(hash function)를 통해 해시(hash)로 변경이 되며 해시는 값(value)과 매칭되어 저장소에 저장이 된다.
여기서 키(Key) 값을 해시 함수(Hash Function)라는 수식에 대입시켜 계산한 후 나온 결과(=hash)를 주소로 사용하여 바로 값(Value)에 접근하게 할 수 하는 방법이 해싱(Hashing)이다.
- 키
- 고유한 값이며, 해시 함수의 input
- 길이가 다양하여 원 상태로 저장하기 위해서는 다양한 길이의 저장소를 구성해야 한다.
- 따라서, 해시함수로 값을 바꾸어 저장이 되어야 공간의 효율성을 추구할 수 있다.
- 해시함수
- 키(key)를 해시(hash)로 바꿔주는 역할
- 다양한 길이의 key -> 일정한 길이의 hash로 변경하여 저장소를 효율적으로 운영
- 다만, 서로 다른 key가 같은 hash가 되는 경우를 해시 충돌(hash collision), 해시 충돌을 일으키는 확률을 최대한 줄이는 함수를 만드는 것이 중요
- 해시
- 해시 함수의 결과물
- 저장소에서 값과 매칭되어 저장
- 값
- 저장소에 최종적으로 저장되는 값
- 키와 매칭되어 저장, 삭제, 검색, 접근이 가능해야 한다.

위의 그림은 n%7의 해시함수를 이용하여 저장하는 것을 보여주고 있다.
Insertion(저장)
7로 나눈 나머지가 해시(hash), 처음 나눠진 76과 같은 input이 키(key), 미리 준비해 놓은 0, 1, 2, 3, 4, 5, 6의 저장소에서 알맞은 hash값을 찾아 value를 저장
- 저장의 시간복잡도는 O(1)
- 키(Key)는 고유하기 때문에 결과로 나온 hash와 값을 넣으면 되기 때문
- 최악의 경우 O(n)이 될 수 있는데 해시 충돌로 인한 모든 value들을 찾아 봐야 하는 경우
Deletion(삭제)
저장되어 잇는 값을 삭제할 때는 저장소에서 해당 key와 매칭되는 값을 찾아 삭제
- 삭제의 시간복잡도는 O(1)
- 키(Key)는 고유하기 때문에 결과로 나온 hash와 값을 삭제하면 되기 때문
- 최악의 경우 O(n)이 될 수 있는데 해시 충돌로 인한 모든 value들을 찾아 봐야 하는 경우
Search(검색)
삭제와 비슷한 과정 - 키로 hash를 구한 후 value를 찾는다.
- 검색의 시간복잡도는 O(1)
- 키(Key)는 고유하기 때문에 결과로 나온 hash와 값을 검색하면 되기 때문
- 최악의 경우 O(n)이 될 수 있는데 해시 충돌로 인한 모든 value들을 찾아 봐야 하는 경우
# 해시 충돌
- 해시테이블은 과정에서 평균 O(1)의 시간복잡도를 가지고 있어 자료구조의 효율성 측면에서 매우 우수
- 다만, 무한한 값(KEY)을 유한한 값(Hash)로 표현하면서 서로 다른 두 개 이상의 유한한 값이 동일한 출력 값을 가지게 되는 해시충돌은 필연적으로 나타날 수 있는 문제이다.

이를 해결하기 위한 방법으로는
Collision Resuloution
1. Separate Chaining(= Chaining)

- 체이닝이란 저장소에서 충돌이 일어나면, 해당 값을 기존 값과 연결시키는 기법
- 위에서 존 뒤에 산다라를 연결시켰는데 이 때, 연결리스트(Linked List) 자료구조를 이용한다.
- 장점
- 한정된 저장소를 효율적 사용
- 해시 함수를 선택하는 중요성이 상대적으로 작아진다.
- 상대적 적은 메모리 - 미리 공간 잡을 필요 x
- 단점
- 한 Hash에 자료들이 계속 연결된다면 검색 효율을 낮출 수 있다.
- 외부 저장 공간 사용하기 때문에 공간 작업 추가로 해야한다.
- 시간복잡도
- 해시 테이블의 저장소 길이 =n, 키의 수 = m 이라고 할 때, 평균 m/n의 키가 들어있는데 a(alpha)라고 정의하자.
- insertion
- 충돌 발생 시, Head에 자료 저장시 O(1)
- Tail에 자료 저장시, 모든 연결리스트를 지나서 접근 하기 때문에 O(a)
- 최악의 경우 O(n)
- deletion & search
- 산출된 hash의 연결리스트 차례로 보기 때문에 O(a)
- 최악의 경우 O(n)
2. Open Addressiong(개방 주소법)
- 해시가 변경되지 않았던 chaining과는 달리 비어있는 hash를 찾아 저장
- 따라서, 1개의 해시와 1개의 값이 매칭되어 있는 형태 유지
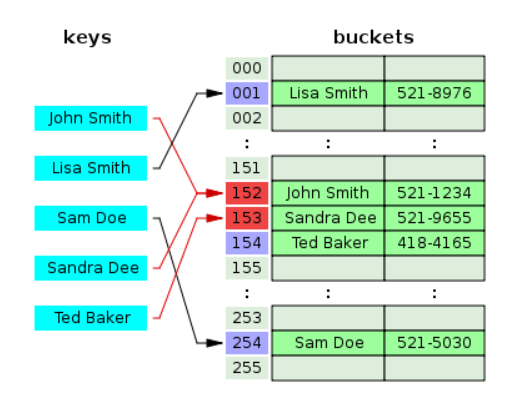
체이닝과는 달리 비어있던 153번에 산다라가 들어가게 되었다. 뒤에 있던 Ted의 해시도 산다라가 저장되어 있어 그 다음 해시에 저장하였다.
과정
- 선형 탐색(Linear Probing) : 다음 해시나 n개를 건너뛰어 비어있는 해시에 데이터 저장
- 제곱 탐색(Quadratic Probing): 충돌이 일어난 해시의 제곱을 한 '해시'에 데이터를 저장
- 이중 해시(Double Hashing): 다른 해시함수를 한 번 더 적용한 해시에 데이터를 저장
장, 단점 및 시간 복잡도
- 장점
- 또 다른 저장공간 없이 해시테이블 내에서 데이터 저장 및 처리가 가능
- 또 다른 저장공간에서의 추가적인 작업이 없다.
- 단점
- 해시 함수의 성능에 전체 해시테이블의 성능이 좌지우지된다.
- 데이터의 길이가 늘어나면 그에 해당하는 저장소를 마련해 두어야 한다.
- 시간 복잡도
- 체이닝의 a(alpha)를 개방 주소법에도 적용한다면, a는 1보다 작거나 같다.
- Insertion & Deletion & Search
- 모두 최상의 경우 O(1) ~ 최악의 경우 O(n)
2. Hash Table의 단점 및 활용
- 순서가 있는 배열에는 어울리지 않는다.
- 상하관계, 순서가 중요한 데이터의 경우 어울리지 않는다.
- 순서와 상관없이 key만을 가지고 hash를 찾아 저장하기 때문
- 공간 효율성이 떨어진다.
- 데이터가 저장되기 전 미리 저장공간 확보
- 공간이 부족하거나 아예 채워지지 않은 경우가 생길 가능성
- Hash Function의 의존도가 높다.
- 평균 데이터 처리 O(1)이지만, 해시 함수의 연산을 고려하지 않는 결과
- 즉, 해시 함수가 매우 복잡하다면 모든 연산의 시간 효율성은 증가
우리가 사용하는 파이썬에서는 방금 알아본 Hash구조와 똑같이 생긴 Dictionary도 있지만 또 한 가지가 더 있다!
ㅏ로 set 자료형 또한 Hash table로 구성된다.
- 따라서, 반복 - 순서가 필요없는, 메모리보다 시간 효율성이 중요한 경우 set 또는 dictionary를 이용하는 것이
- list를 이용하는 것 보다 좋다는 것을 기억해주자!!
- 각 상황에 맞는 자료형, 자료구조를 이용하는 것이 좋은 개발자가 되는 첫 걸음이라고 생각이 든다!!
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 트리 2 - 이진 탐색 트리 with Python (0) | 2022.09.15 |
|---|---|
| [자료구조] 트리 (Tree) 1 with Python (1) | 2022.09.13 |
| [자료구조] 큐(Queue)활용 - 버퍼(Buffer), deque with Python (0) | 2022.09.09 |
| [자료구조] 큐(Queue) - 선형 큐, 원형 큐, 우선순위 큐 with Python (0) | 2022.09.09 |
| [자료구조] Stack with Python (0) | 2022.09.09 |
