728x90
목차
- 팬윅 트리?
- 구현
- 업데이트
1. Fenwick Tree ?
- Segment Tree 처럼 구간에 대한 연산을 저장하는 트리
- Segment Tree 보다 적은 메모리로 사용 가능하다!!
- 절반 정도의 메모리만으로 사용 가능
- 시간 복잡도 O(logN)
- 비트를 이용한 구간 연산을 진행한다.




Q. 3~5번째 인덱스 구간 합을 구하기
A. 두 구간의 차를 구하면 된다.

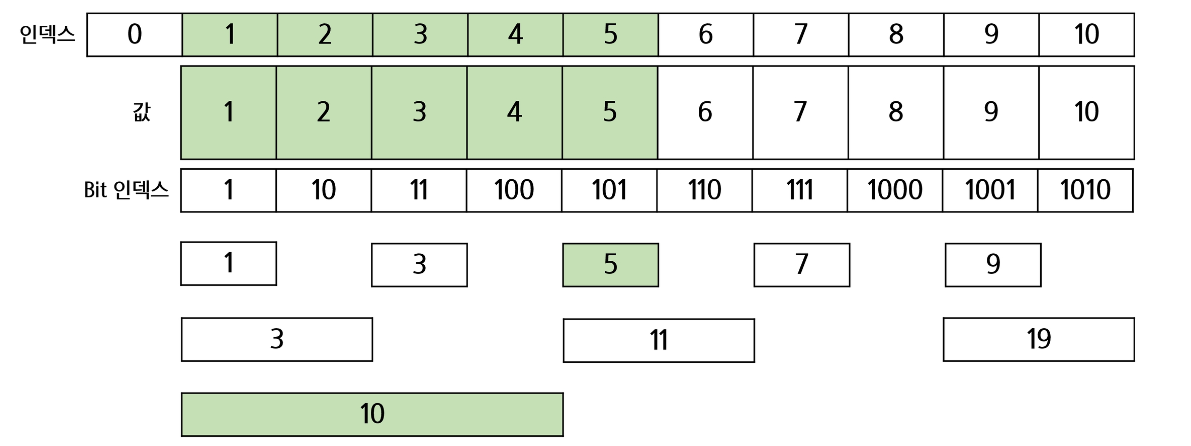
5번 인덱스까지의 값을 구하려면 2진수 101 인덱스 값과 100 인덱스 값을 더하면 된다.
101 인덱스에서 마지막 1의 값을 제거해주면 100이 된다.
Q. 마지막 2진수 1의 값을 제거하는 방법은?


Answer.
- N = N - (N & -N)
- 5 - ( 5 & -5 ) = 4
- 4 - ( 4 & -4 ) = 0
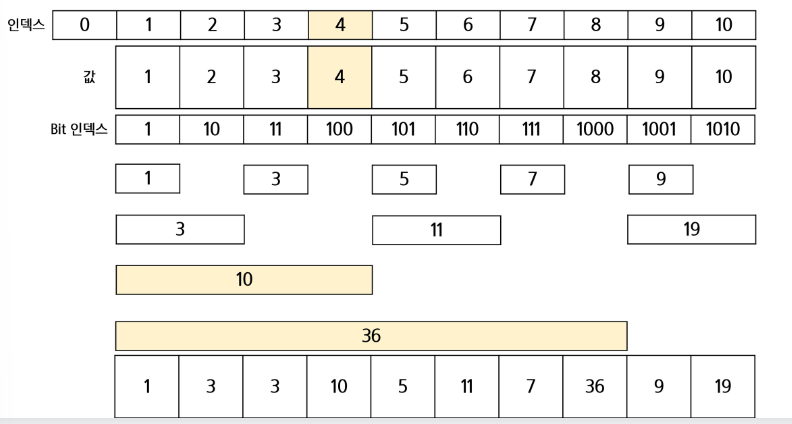
2. 구현

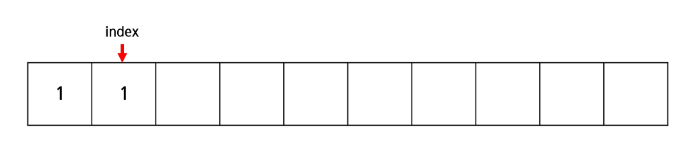
- Val = 1
- index = 1 -> 1 += (1 & -1) = 2

- Val = 1
- index = 2 -> 2 += (2 & -2) = 4
- Val = 1
- index = 4 -> 4 += (4 & -4) = 8

- Val = 1
- index = 8 -> 8 += (8 & -8) = 16
- 트리의 길이보다 index 값이 크기 때문에 중지


- Val = 2
- index = 2 -> 2 += (2 & -2) = 4

- Val = 2
- index = 4 -> 4 += (4 & -4) = 8

- Val = 2
- index = 8 -> 8 += (8 & -8) = 16
- 트리의 길이보다 index 값이 크기 때문에 중지


- Val = 3
- index = 3 -> 3 += (3 & -3) = 4

- Val = 3
- index = 4 -> 4 += (4 & -4) = 8

- Val = 3
- index = 8 -> 8 += (8 & -8) = 16
- 트리의 길이보다 index 값이 크기 때문에 중지

- Val = 4
- index = 4 -> 4 += (4 & -4) = 8

- Val = 4
- index = 8 -> 8 += (8 & -8) = 16
- 트리의 길이보다 index 값이 크기 때문에 중지

- Val = 5
- index = 5 -> 5 += (5 & -5) = 6

- Val = 5
- index = 6 -> 6 += (6 & -6) = 8

- Val = 5
- index = 8 -> 8 += (8 & -8) = 16
- 트리의 길이보다 index 값이 크기 때문에 중지

- Val = 6
- index = 6 -> 6 += (6 & -6) = 8
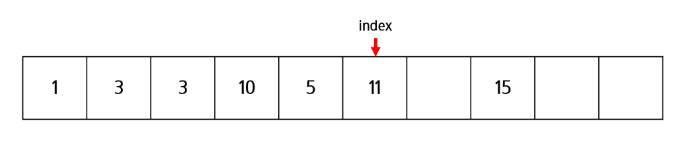
- Val = 6
- index = 8 -> 8 += (8 & -8) = 16
- 트리의 길이보다 index 값이 크기 때문에 중지

- Val = 7
- index = 7 -> 7 += (7 & -7) = 8

- Val = 7
- index = 8 -> 8 += (8 & -8) = 16
- 트리의 길이보다 index 값이 크기 때문에 중지

- Val = 8
- index = 8 -> 8 += (8 & -8) = 16
- 트리의 길이보다 index 값이 크기 때문에 중지
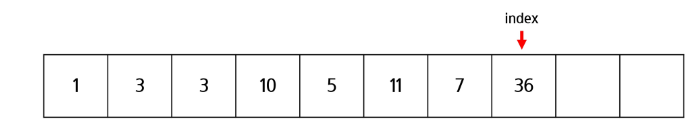
- Val = 9
- index = 9 -> 9 += (9 & -9) = 10

- Val = 9
- index = 10 -> 10 += (10 & -10) = 12
- 트리의 길이보다 index 값이 크기 때문에 중지

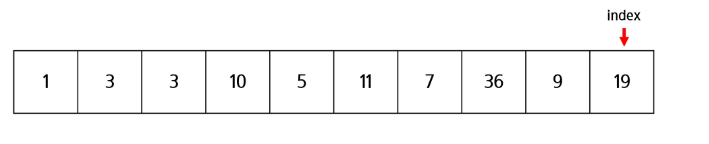
- Val = 10
- index = 10 -> 10 += (10 & -10) = 12
- 트리의 길이보다 index 값이 크기 때문에 중지

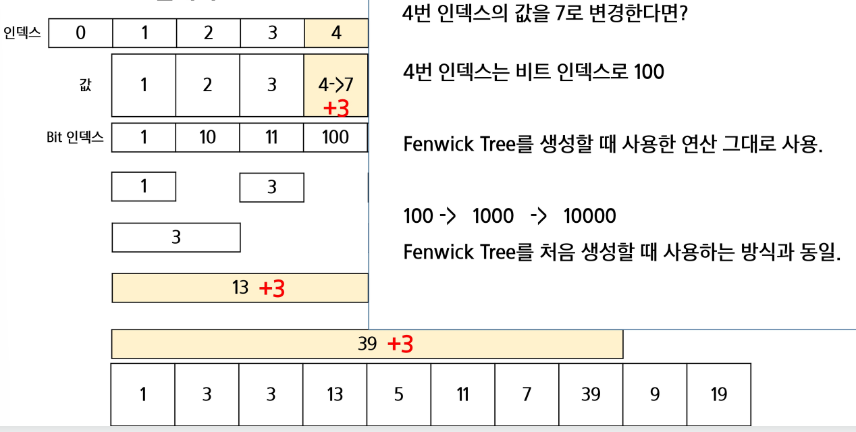
3. 업데이트
특정 값을 변경해주고 싶다면, 0이 아닌 마지막 비트만큼 더하면서 구간들의 값을 변경

전체 코드
import sys
input = sys.stdin.readline()
# 데이터의 개수(n), 변경 횟수(m), 구간 합 계산 횟수(k)
n,m,k = map(int,input().split())
# 전체 데이터의 개수는 최대 1,000,000개
arr = [0] * (n+1)
tree = [0] * (n+1)
# i번째 수까지의 누적 합을 계산하는 함수
def prefix_sum(i):
result = 0
while i > 0:
result += tree[i]
# 0이 아닌 마지막 비트만큼 빼가면서 이동
i -= (i & -i)
return result
# i번째 수를 dif만큼 더하는 함수
def update(i,dif):
while i <= n:
tree[i] += dif
i += (i & -i)
# start부터 end까지의 구간 합을 계산하는 함수
def interval_sum(start,end):
return prefix_sum(end) - prefix_sum(start-1)
for i in range(m+k):
a,b,c = map(int,input().split())
# 업데이트(update) 연산인 경우
if a == 1:
update(b,c - arr[b])
arr[b] = c
# 구간 합(interval) 연산인 경우
else:
print(interval_sum(b,c))
728x90
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 시간복잡도 정리 with Cpp (0) | 2023.02.24 |
|---|---|
| [자료구조] 그래프 with Python (0) | 2022.09.28 |
| [자료구조] 힙(heap) with Python (0) | 2022.09.15 |
| [자료구조] 트리 2 - 이진 탐색 트리 with Python (0) | 2022.09.15 |
| [자료구조] 트리 (Tree) 1 with Python (1) | 2022.09.13 |
