지금까지 여러 자료 구조를 알아보았고, 아마 이번에 배우는 그래프가 마지막일 것이다!
목차
- 그래프란?
- 그래프 유형
- 그래프 표현
- 서로소 집합
1. 그래프란?
- 그래프는 아이템(사물 또는 추상적 개념)들과 이들 사이의 연결 관계를 표현
- 정점(Vertex)들의 집합과 이들을 연결하는 간선(Edge)들의 집합으로 구성된 자료 구조
- IVI : 정점의 개수
- IEI : 그래프에 포함된 간선의 개수
- 무향 그래프 - IVI 개의 정점을 가지는 그래프는 최대 IVI (IVI - 1) / 2 간선이 가능
- 유향 그래프 - IVI 개의 정점을 가지는 그래프는 최대 IVI (IVI - 1) 간선이 가능
- 선형 자료구조나 트리 자료구조로 표현하기 어려운 N:N 관계를 가지는 원소들을 표현하기에 용이
2. 그래프 유형
1. 무향 그래프 (Undirected Graph)

2. 유향 그래프 (Directed Graph)

3. 가중치 그래프

4. 사이클 없는 방향 그래프 (DAG, Directed Acyclic Graph)

a. 완전 그래프
- 정점들에 대해 가능한 모든 간선들을 가진 그래프

b. 부분 그래프
- 원래 그래프에서 일부의 정점이나 간선을 제외한 그래프
트리와 그래프의 차이
모양이 비슷한 둘이지만, 엄연한 차이가 존재한다.
- 트리 - 엄격한 상하 관계
- 간선에 방향이 정해져 있고, 부모-자식 관계가 존재
- 노드끼리 원형을 이룰 수 없다.
- 그래프 - 평등 관계
- 부모-자식 관계 xx
- 또한, 노드끼리 원형을 이룰 수 있음
- 트리는 그래프의 특별한 형태 (1:N) 관계로 볼 수 있다.
- 사이클이 있는 무향 그래프
인접(Adjacency)
- 두 개의 정점에 간선이 존재(연결됨)하면 서로 인접해 있다고 한다.
- 완전 그래프에 속한 임의의 두 정점들은 모두 인접해 있다.

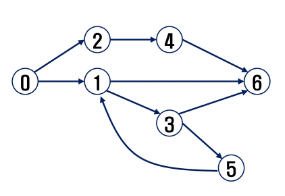
그래프 경로
- 경로란 간선들을 순서대로 나열한 것
- 간선들 : (0,2), (2,4), (4,6)
- 정점들: 0 - 2 - 4 - 6
- 경로 중 한 정점을 최대한 한 번만 지나는 경로를 단순경로라 한다.
- 0 - 2 - 4 - 6, 0 - 1 - 6
- 시작한 정점에서 끝나는 경로를 사이클(Cycle)이라고 한다.
- 1 - 3 - 5 - 1
3. 그래프 표현
- 간선 정보를 저장하는 방식, 메모리나 성능을 고려해서 결정
- 인접 행렬 (Adjacent matrix)
- IVI x IVI 크기의 2차원 배열을 이용해서 간선 정보를 저장
- 배열의 배열(포인터 배열)
- 인접 리스트 (Adjacent List)
- 각 정점마다 해당 정점으로 나가는 간선의 정보를 저장
- 간선의 배열
- 간선(시작 정점, 끝 정점)을 배열에 연속적으로 저장
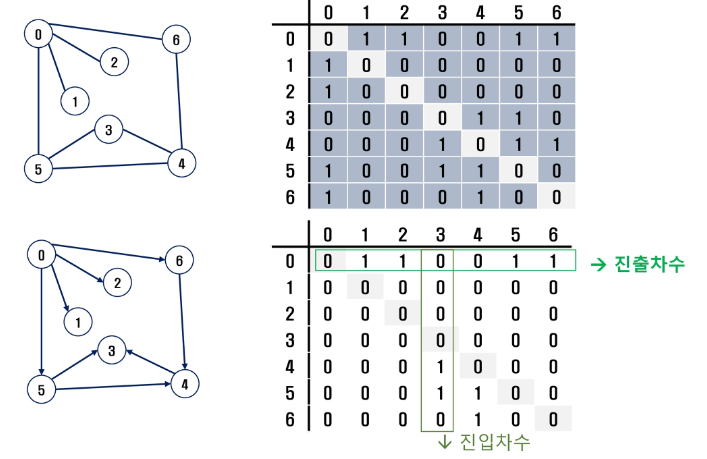
인접 행렬
- 두 정점을 연결하는 간선의 유무를 행렬로 표현
- IVI x IVI 정방 행렬
- 행 번호와 열 번호는 그래프의 정점에 대응
- 두 정점이 인접되어 있으면 1, 그렇지 않으면 0으로 표현
- 무향 그래프
- i 번째 행의 합 = i 번째 열의 합 = Vi의 차수 = 연결되어 있는 간선의 수
- 유향 그래프
- 행 i의 합 = Vi의 진출 차수
- 열 i의 합 = Vi의 진입 차수
- 단점
- 희소 그래프 (sparse graph) - 정점은 1000개가 있는데 간선은 5개뿐인 그래프처럼 간선의 수가 적은 그래프
- 그래프의 정점은 상대적으로 많고 간선은 그에 비해 적다.
- 공간의 낭비가 발생
- 탐색 할 때도 비효율적
- 5개의 간선을 기록하기 위해서 1000 x 1000의 행렬을 사용해야 함
- 희소 그래프 (sparse graph) - 정점은 1000개가 있는데 간선은 5개뿐인 그래프처럼 간선의 수가 적은 그래프
- 장점
- 밀집 그래프 (dense graph) - 반대로 간선의 수가 정점에 비해 많은 그래프
- 정점과 그에 따른 간선의 개수가 비례해서 많다 (= 완전 그래프)
- 자기 자신만 빼고 다 채워져 있다.
- 인덱스를 이용하므로 다른 정점과 연결되었는지 파악할 때 유리하다.
- 밀집 그래프 (dense graph) - 반대로 간선의 수가 정점에 비해 많은 그래프
- 시간 및 공간 복잡도
- 정점의 인접 노드 탐색 시간 복잡도 - O(1)
- 공간 복잡도 - O(V^2)
- 전체 간선 체크 시간 복잡도 - O(N^2)
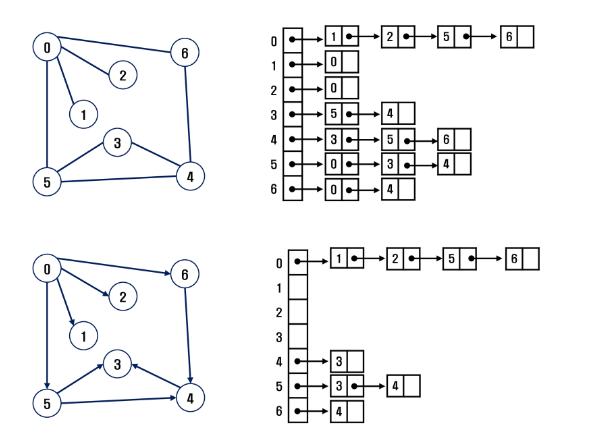
인접 리스트
- 각 정점에 대한 인접 정점들을 순차적으로 표현
- 하나의 정점에 대한 인접 정점들을 각각 노드로 하는 연결 리스트로 저장
- 포인터의 역할일 뿐이지 이어져있다고 연결된 게 아니다.
- 무향 그래프
- 전체 노드 수 = 전체 간선의 수 * 2
- 각 정점의 노드 수 = 정점의 차수
- 유향 그래프
- 전체 노드 수 = 전체 간선의 수
- 각 정점의 노드 수 = 정점의 진출 차수
- 장점
- 인접 행렬에서 희소그래프의 단점을 해결
- 공간, 시간 복잡도가 인접 행렬보다 훨씬 효율적
- 인접 행렬에서 희소그래프의 단점을 해결
- 시간 복잡도
- 간선의 개수만큼 메모리 공간이 필요 - O(E)
- 다른 노드까지의 가중치를 알아내는 시간 - O(V)
다익스트라 알고리즘 - 인접 리스트 활용
플로이드 알고리즘 - 인접 행렬 활용
- 정점의 개수가 작으면 플로이드 알고리즘
- 정점과 간선의 개수가 많으면 우선순위 큐를 이용하는 다익스트라 알고리즘 이용하면 유리
# 그래프 탐색 방법
아래 2가지 방법이 존재하는데 잘 모른다면 이전 글 참고!
- DFS
- BFS
2022.08.17 - [ALGORITHM/알고리즘 알아보기] - [알고리즘] DFS(깊이 우선 탐색)
[알고리즘] DFS(깊이 우선 탐색)
1ㄷ1 관계는 선형구조라고 불렀고 1ㄷN의 관계는 트리라고 불렀다. 그럼 N:N의 관계는 어떤 구조일까? 바로 그래프 구조라고 부른다. 비선형 구조인 그래프 구조는 그래프로 표현된 모든 자료를
cheon2308.tistory.com
2022.08.24 - [ALGORITHM/알고리즘 알아보기] - [알고리즘] Queue를 활용한 깊이 우선 탐색(BFS)
[알고리즘] Queue를 활용한 깊이 우선 탐색(BFS)
그래프를 탐색하는 방법에는 크게 두 가지가 있다. 깊이 우선 탐색(Depth First Search, DFS) 저번에 봤듯이 Stack 또는 재귀의 단계를 활용하여 구현 너비 우선 탐색(Breadth First Search, BFS) 탐색 시작점의..
cheon2308.tistory.com
4. 서로소 집합 (분리 집합)
- 서로소 또는 상호배타 집합들은 서로 중복 포함된 원소가 없는 집합
- 즉, 교집합이 없다.
- 집합에 속한 하나의 특정 멤버를 통해 각 집합들을 구분
- 대표자(representative)
- 연결 리스트 또는 트리를 이용하여 표현
- 연산
- Make-Set(x) - 특정 원소를 대표자로하는 집합 생성
- Find-Set(x) - 특정 원소가 어떤 집합에 속해있는지 알려준다.
- Union(x,y) - 두 집합을 하나의 집합으로 합쳐준다.
표현
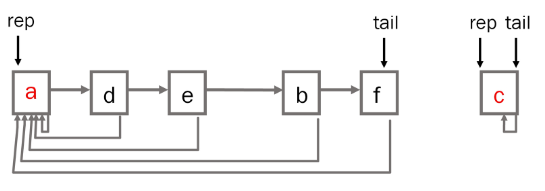
1. 연결리스트
- 같은 집합의 원소들은 하나의 연결리스트로 관리
- 연결리스트의 맨 앞의 원소를 집합의 대표 원소로 삼는다.
- 각 원소는 집합의 대표원소를 가리키는 링크를 갖는다.
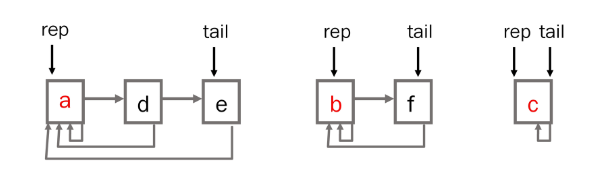
- 연산 예
- Find-set(e) -> return a
- Union(a,b)
2. 트리
- 하나의 집합(a disjoint set)을 하나의 트리로 표현
- 자식 노드가 부모 노드를 가리키며 루트 노드가 대표자가 된다.
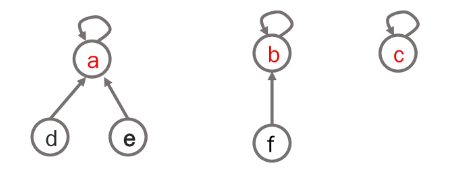
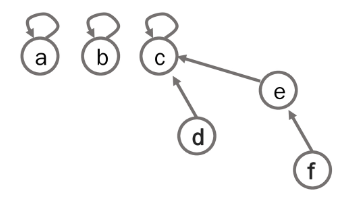
- 연산 예
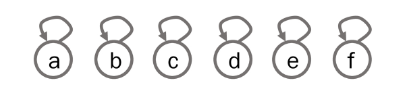
- Make-Set(a) ~ Make-Set(f)
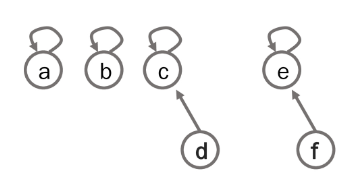
- Union(c,d), Union(e,f)
- Union(d,f)
- Find-Set(d) - return c
- Find-Set(e) - return c
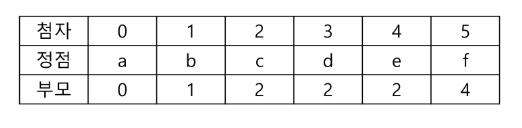
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 노드의 개수와 간선(Union 연산)의 개수 입력 받기
v, e = map(int, input().split())
parent = [0] * (v + 1) # 부모 테이블 초기화하기
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
parent[i] = i
# Union 연산을 각각 수행
for i in range(e):
a, b = map(int, input().split())
union_parent(parent, a, b)
# 각 원소가 속한 집합 출력하기
print('각 원소가 속한 집합: ', end='')
for i in range(1, v + 1):
print(find_parent(parent, i), end=' ')
print()
# 부모 테이블 내용 출력하기
print('부모 테이블: ', end='')
for i in range(1, v + 1):
print(parent[i], end=' ')
연산의 효율 높이기
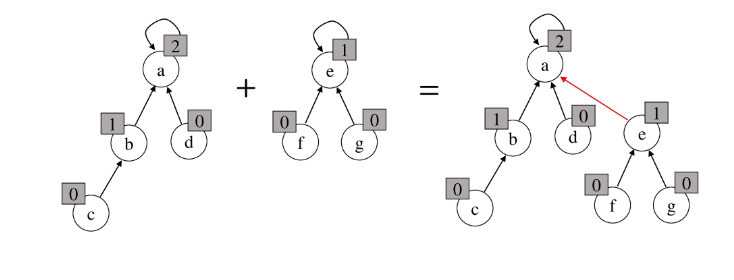
- Rank를 이용한 Union
- 각 노드는 자신을 루트로 하는 subtree의 높이를 랭크 Rank라는 이름으로 저장한다
- 두 집합을 합칠 때 rank가 낮은 집합을 rank가 높은 집합에 붙인다.
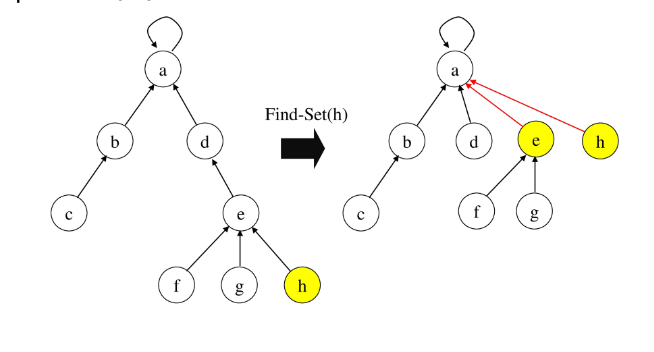
- Path compression
- Find-Set을 행하는 과정에서 만나는 모든 노드들이 직접 root를 가리키도록 포인터를 바꾸어 준다.
# rank 이용 예시
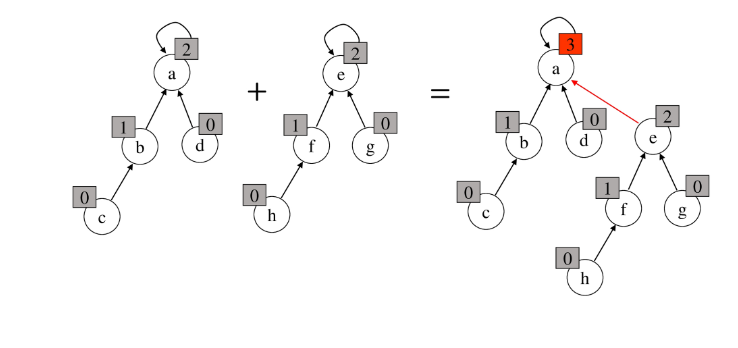
# path compression 예
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 시간복잡도 정리 with Cpp (0) | 2023.02.24 |
|---|---|
| [자료구조] Fenwick Tree(Binary Indexed Tree, BIT) with Python (0) | 2022.11.30 |
| [자료구조] 힙(heap) with Python (0) | 2022.09.15 |
| [자료구조] 트리 2 - 이진 탐색 트리 with Python (0) | 2022.09.15 |
| [자료구조] 트리 (Tree) 1 with Python (1) | 2022.09.13 |
