728x90
저번에 배웠던 버블, 선택 정렬은 비교와 교환에 기반한 정렬 방식이었고 카운팅 정렬은 비교환 방식이었다.
이번엔 분할 정복 알고리즘에 기반한 퀵 정렬과 합병 정렬에 대해서 알아보자.
# 합병 정렬
- 컴퓨터에 관해 일을 한다면 꼭 알아야 되는 '존 폰 노이만'이 제안한 방법
- 일반적으로 구현 시 중복된 값을 입력 순서와 동일하게 정렬하는 '안정 정렬'
- 하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법
과정
- 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 보고 그렇지 않다면 리스트를 절반으로 자른다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬하고 다시 하나의 정렬된 리스트로 합병
- 추가적인 리스트가 필요하며 각 부분 배열을 정렬할 때도 합병 정렬을 순환적으로 호출하여 적용
- 실제로 정렬이 이루어지는 시점은 2개의 리스트를 합병(merge)하는 단계

특징
- 장점
- 안정적인 정렬 방법: 데이터 분포에 영향을 덜 받아 정렬되는 시간은 동일 O(nlog2 n)
- 만약 레코드를 연결 리스트로 구성하면 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다. -> 제자리 정렬(추가적인 공간이 필요하지 않음)로 구현할 수 있음
- 따라서 크기가 큰 레코드를 정렬할 경우 연결 리스트를 사용한다면, 합병 정렬은 다른 어떤 정렬 방법보다 효율적
- 단점
- 만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요 -> 제자리 정렬 x
- 레코드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비
def merge_sort(arr):
if len(arr) <= 1: # 더이상 분할 불가
return arr
mid = len(arr) // 2
# 재귀 호출로 분할 : Divide
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
return merge(left, right)
def merge(left, right):
sorted_list = []
# 나눠진 두 배열을 정렬 : Conquer
while 0 < len(left) and 0 < len(right):
if left[0] <= right[0]:
sorted_list.append(left.pop(0))
else:
sorted_list.append(right.pop(0))
# 비교후 남아있는 값 병합 : Merge
sorted_list.extend(left + right)
return sorted_list
print(merge_sort([5, 3, 8, -1, 9, 2]))# 위에 있던 merge 함수에서 수행하는 기능을
# merge_sort 함수에 모두 포함시킨 버전
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
sorted_list = []
while 0 < len(left) and 0 < len(right):
if left[0] <= right[0]:
sorted_list.append(left.pop(0))
else:
sorted_list.append(right.pop(0))
sorted_list.extend(left + right)
return sorted_list
# 퀵 정렬
주어진 배열을 두 개로 분할하고, 각각을 정렬하는 부분에서 합병 정렬과 동일해 보일 수 있다.
차이점
- 합병 정렬은 그냥 두 부분으로 나누는 반면, 퀵 정렬은 분할 시, 기준 아이템(pivot item) 중심으로, 이보다 작은 것이 왼편, 큰 것은 오른편에 위치시킨다.
- 각 부분 정렬이 끝난 후, 합병 정렬은 "합병"이란 후처리 작업이 필요하나, 퀵정렬은 필요로 하지 않는다.
def quick_sort(array, start, end):
if start >= end: # 원소가 1개인 경우 종료
return
pivot = start # 피벗은 첫 번째 원소
left = start + 1
right = end
while(left <= right):
# 피벗보다 큰 데이터를 찾을 때까지 반복
while(left <= end and array[left] <= array[pivot]):
left += 1
# 피벗보다 작은 데이터를 찾을 때까지 반복
while(right > start and array[right] >= array[pivot]):
right -= 1
if(left > right): # 엇갈렸다면 작은 데이터와 피벗을 교체
array[right], array[pivot] = array[pivot], array[right]
else: # 엇갈리지 않았다면 작은 데이터와 큰 데이터를 교체
array[left], array[right] = array[right], array[left]
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
quick_sort(array, start, right - 1)
quick_sort(array, right + 1, end)
quick_sort(array, 0, len(array) - 1)
print(array)
- 파이썬 장점을 살린 퀵 정렬
array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
def quick_sort(array):
# 리스트가 하나 이하의 원소만을 담고 있다면 종료
if len(array) <= 1:
return array
pivot = array[0] # 피벗은 첫 번째 원소
tail = array[1:] # 피벗을 제외한 리스트
left_side = [x for x in tail if x <= pivot] # 분할된 왼쪽 부분
right_side = [x for x in tail if x > pivot] # 분할된 오른쪽 부분
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬을 수행하고, 전체 리스트를 반환
return quick_sort(left_side) + [pivot] + quick_sort(right_side)
print(quick_sort(array))
과정
예제를 통해 살펴보자. {69, 10, 30, 2, 16, 8, 31}
1) 원소의 개수가 8개이므로 네 번째 자리에 있는 원소 2를 첫 번째 피봇으로 선택하고 퀵 정렬 시작
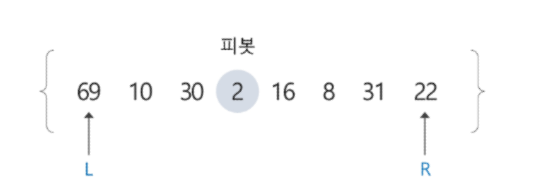
- L이 오른쪽으로 이동하면서 피봇보다 크거나 같은 원소를 찾고, R은 왼쪽으로 이동하면서 피봇보다 작은 원소를 찾는다.
- L은 원소 69를 찾았지만, R은 피봇보다 작은 원소를 찾지 못한 채로 원소 69에서 L과 만나게 됨
- L과 R이 만났으므로, 원소 69를 피봇과 교환하여 피봇 원소 2의 위치를 확정
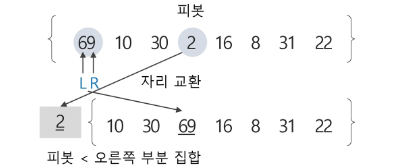
2) 피봇 2의 왼쪽 부분 집합은 공집합이므로 퀵 정렬 수행 x, 오른쪽 부분 집합에 대해 퀵 정렬 수행
- 오른쪽 부분 집합의 원소가 7개 이므로 가운데 있는 원소 16을 피봇으로 선택.
- L이 찾은 30과 R이 찾은 8을 서로 교환한다.
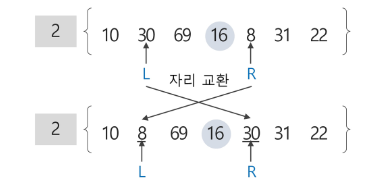
- 현재 위치에서 L과 R의 작업을 반복한다.
- L은 원소 69를 찾았지만, R은 피봇보다 작은 원소를 찾지 못한 채로 원소 69에서 L과 만난다.
- L과 R이 만났으므로, 원소 69를 피봇과 교환하여 피봇 원소 16의 위치를 확정
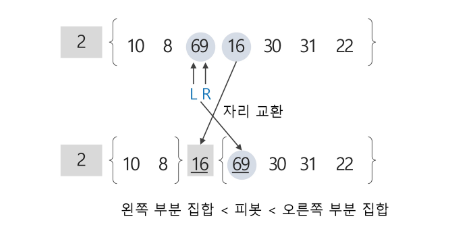
3) 피봇 16의 왼쪽 부분 집합에서 원소 10을 피봇으로 선택하여 퀵 정렬 수행
- L의 원소 10과 R의 원소 8을 교환하는데, L의 원소가 피봇이므로 피봇 원소에 대한 자리 교환이 발생한 것이므로 교환한 자리를 피봇 원소 10의 위치로 확정한다.
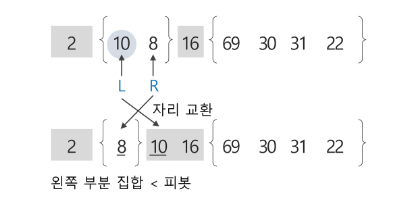
4) 피봇 10의 확정된 위치에서의 왼쪽 부분 집합은 원소가 한 개 이므로 퀵 정렬을 수행하지 않고, 오른쪽 부분 집합은 공집합이므로 역시 퀵 정렬을 수행하지 않는다.
- 이제 1단계 의 피봇이었던 16에 대한 오른쪽 부분집합에 대해 퀵 정렬 수행
- 원소가 4개이므로 두 번째 원소 30 피봇으로 선택
- L이 찾은 69와 R이 찾은 22를 서로 교환
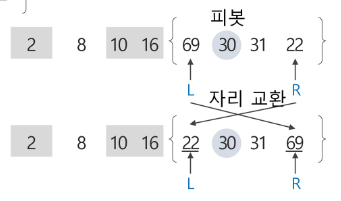
- 현재 위치에서 L과 R의 작업 반복한다. L은 오른쪽으로 이동하면서 피봇보다 크거나 같은 원소인 30을 찾고, R은 왼쪽으로 이동하면서 피봇 보다 작은 원소를 찾다가 못 찾고 원소 30에서 L과 만난다.
- L과 R이 만났으므로 피봇과 교환한다. 이경우는 R의 원소가 피봇이므로 피봇에 대한 자리 교환이 발생한 것이므로 교환한 자리를 피봇의 자리로 확정한다.

5) 피봇 30의 확정된 위치에서의 왼쪽 부분 집합의 원소가 한 개 이므로 퀵 정렬을 수행하지 않고, 오른쪽 부분 집합에 대해서 퀵 정렬 수행.
- 오른쪽 부분 집합의 원소 2개 중에서 원소 31을 피봇으로 선택한다.
- L은 오른쪽으로 이동하면서 원소 31을 찾고, R은 왼쪽으로 이동하면서 피봇보다 작은 원소를 찾다가 못 찾은 채로 원소 31에서 L과 만난다. L과 R이 만났으므로 피봇과 교환하는데 R의 원소가 피봇이므로 결국 제자리가 확정된다.
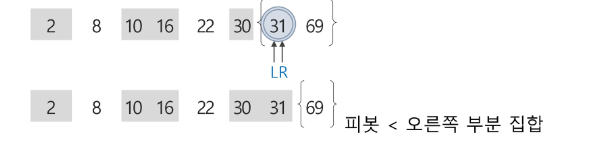
- 피봇 31의 오른쪽 부분 집합의 원소가 한 개 이므로 퀵 정렬을 수행하지 않는다.
- 이로써 전체 퀵 정렬 완성
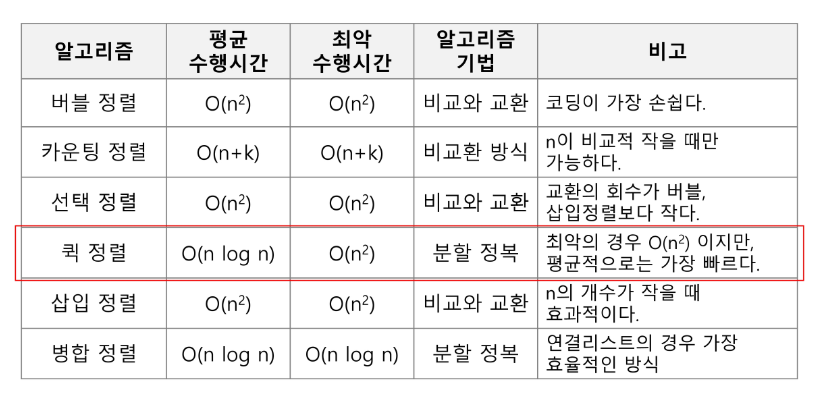
퀵 정렬의 최악의 시간 복잡도는 O(n^2)로, 합병 정렬에 비해 좋지 못하지만, 평균 복잡도는 nlogn이다
728x90
'ALGORITHM > 알고리즘 알아보기' 카테고리의 다른 글
| [알고리즘] 다익스트라 알고리즘 (1) | 2022.09.23 |
|---|---|
| [알고리즘] 반복문과 재귀 (1) | 2022.09.21 |
| [알고리즘] 정렬1 - 버블, 카운팅, 선택 정렬 (0) | 2022.09.09 |
| [Algorithm] 최장 증가 수열 (LIS) (0) | 2022.09.07 |
| [알고리즘] Queue를 활용한 깊이 우선 탐색(BFS) (0) | 2022.08.24 |
