728x90
지금까지 알고리즘을 풀면서 재귀와 반복문은 많이 사용했을 것이다. 똑같은 상황에서 사용가능 한 이 두가지 방법을 언제 사용하는 것이 좋은지 알아보자.
목차
1. 재귀?
2. 반복문
3. 비교
1. 재귀(Recursion)
우선 재귀를 사용하기 위해서 수학적 귀납법 증명에 대해 간단히 알아보자.
- n이 0일 때 문제를 풀 수 있고
- n-1에서 문제를 풀 수 있으면 n에서도 문제를 풀 수 있다
- 위의 2가지가 사실이면 모든 가능한 n에 대해 문제를 풀 수 있다는 것이 사실!!
이렇게 프로그램을 돌리면 순차적인 코드에서와 마찬가지로 필요한 계산이 완전히 동일하지만 단순히 표현하는 방법이 달라지는 것

재귀
위의 수학적 귀납법의 풀이 과정을 이용한 것이 재귀이다.
- 재귀는 주어진 문제의 해를 구하기 위해 동일하면서 더 작은 문제의 해를 이용하는 방법
- 하나의 큰 문제를 해결할 수 있는 (해결하기 쉬운) 더 작은 문제로 쪼개고 결과들을 결합한다.
- 재귀적 정의
- 하나 또는 그 이상의 기본 경우(basis case or rule)
- 집합에 포함되어 있는 원소로 induction을 생성하기 위한 시드(seed) 역할
- 하나 또는 그 이상의 유도된 경우(inductive case or rule)
- 새로운 집합의 원소를 생성하기 위해 결합되어지는 방법
- 하나 또는 그 이상의 기본 경우(basis case or rule)
- 재귀 함수 (recursive function)
- 함수 내부에서 직접 혹은 간접적으로 자기 자신을 호출하는 함수
- 일반적으로 재귀적 정의를 이용해서 재귀 함수를 구현
- 따라서, 기본 부분(basis part)와 유도 부분(inductive part)로 구성된다.
- 재귀적 프로그램을 작성하는 것은 반복 구조에 비해 간결하고 이해하기 쉽다(가독성)
- 아직 익숙하지 않은 개발자들은 재귀적 프로그램이 어렵다고 느낀다.
- 함수 호출은 프로그램 메모리 구조에서 스택을 사용한다. 따라서, 재귀 호출은 반복적인 스택의 사용을 의미하며 메모리 및 속도에서 성능저하 발생
- 또한, 재귀를 사용하면 변수의 사용을 줄여 mutable한 상황을 제거하게 되어, 시스템 오류의 발생 가능성을 줄일 수 있다.
팩토리얼 재귀 함수
- 재귀적 정의
- Basis rule - N<=1인 경우, n = 1
- Inductive rule - N>1, n! = n X (n-1)!
- n!에 대한 재귀함수
def fact(n):
if n<=1:
return 1 # basis part
else:
return n*fact(n-1) # inductive part

- 하지만 위와 같은 코드는 재귀의 단점 -> 스택오버플로우가 발생하며, 성능도 느려진다.
- 따라서, 꼬리 재귀를 이용해 문제점을 어느정도 해결하며 성능 및 메모리의 이점을 얻을 수 있다.
- 프로그래머가 재귀함수를 꼬리 재귀 방식으로 개발
- 컴파일러가 꼬리 재귀 최적화를 지원해야한다.
- 2번이 만족되지 않으면 개발자가 꼬리 재귀 방식으로 개발해도 이점을 얻을 수 없다.
- 꼬리 재귀로 만든 팩토리얼 코드
- 말 그대로 return 문 내에서 연산을 해주지 않게 된다.
def tael_fact(n, acc):
if n<=1:
return acc # basis part
else:
return Tail_Recursive(n-1, n*acc) # inductive part
2. 반복(Iteration)
- 수행하는 작업이 완료될 때 까지 계속 반복
- 루프 (for, while 구조)
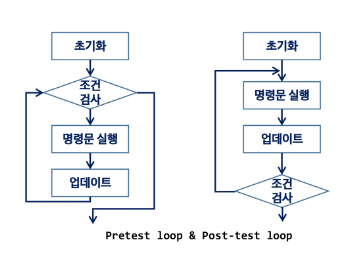
- 반복 구조
- 초기화
- 반복되는 명령문을 실행하기 전에 (한번만) 조건 검사에 사용할 변수의 초기값 설정
- 조건 검사(check control expression)
- 반복할 명령문 실행(action)
- 업데이트(loop update)
- 무한 루프(infinite loop)가 되지 않게 조건이 거짓(false)이 되게 한다.
- 초기화
반복문을 이용해서 앞전에 배웠던 선택정렬을 구현해 보자.
def SelectionSort(A):
n = len(A)
for i in range(0, n-1):
minI = i
for j in range(i+1, n):
if A[j] < A[minI]
minI = j
A[minI], A[i] = A[i], A[minI]
3. 비교
- 해결할 문제를 고려해서 반복이나 재귀의 방법을 선택
- 재귀는 문제 해결을 위한 알고리즘 설계가 간단하고 자연스럽다.
- 추상 자료형 (list, tree 등)의 알고리즘은 재귀적 구현이 간단하고 자연스러운 경우가 많다.
- 일반적으로, 재귀적 알고리즘은 반복(Iterative) 알고리즘보다 더 많은 메모리와 연산을 필요로 한다.
- 즉, 입력 값 n이 커질수록 재귀 알고리즘은 반복에 비해 비효율적일 수 있다.

- 2**k 연산에 대한 재귀와 반복을 살펴보자

728x90
'ALGORITHM > 알고리즘 알아보기' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리 (1) | 2022.09.29 |
|---|---|
| [알고리즘] 다익스트라 알고리즘 (1) | 2022.09.23 |
| [알고리즘] 정렬2 - 합병(병합), 퀵 정렬 (1) | 2022.09.09 |
| [알고리즘] 정렬1 - 버블, 카운팅, 선택 정렬 (0) | 2022.09.09 |
| [Algorithm] 최장 증가 수열 (LIS) (0) | 2022.09.07 |
