728x90
지난 시간의 배열도 그렇고 오늘 배울 정렬은 대체 어떤 것을 위해 배우는 것일까?
그걸 알기 위해 '인덱스'에 대해 조금 알아보고 가자.
인덱스
- 인덱스라는 용어는 데이터베이스에서 유래했으며, 테이블에 대한 동작 속도를 높여주는 자료 구조이다. Database 분야가 아닌 곳에서는 Look up table 등의 용어를 사용하기도 한다.
- 인덱스를 저장하는데 필요한 디스크 공간은 보통 테이블을 저장하는데 필요한 디스크 공간보다 작다. 왜냐하면 인덱스는 키-필드만 갖고 있고, 테이블의 다른 세부 항목들은 갖고 있지 않기 때문이다.
- 배열을 사용한 인덱스
- 대량의 데이터를 매번 정렬하면, 프로그램의 반응은 느려질 수 밖에 없다. 이러한 대량 데이터의 성능 저하 문제를 해결하기 위해 배열 인덱스를 사용

정렬
- 2개 이상의 자료를 특정 기준에 의해 작은 값부터 큰 값(오름차순 : ascending), 혹은 그 반대의 순서대로(내림차순: descending) 재배열하는 것
- 키
- 자료를 정렬하는 기준이 되는 특정 값
- 종류
- 버블 정렬 (Bubble Sort)
- 카운팅 정렬 (Counting Sort)
- 선택 정렬 (Selectiong Sort)
- 퀵 정렬 (Quick Sort)
- 삽입 정렬 (Insertion Sort)
- 병합 정렬 (Merge Sort)
모두 알아보진 않을 거고 몇 가지만 다뤄보자!!
버블 정렬(Bubble Sort)
- 인접한 두 개의 원소를 비교하여 자리를 계속 교환하는 방식
- 정렬 과정
- 첫 번째 원소부터 인접한 원소끼리 계속 자리를 교환하면서 맨 마지막 자리까지 이동한다.
- 한 단계가 끝나면 가장 큰 원소가 마지막 자리로 정렬된다.
- 교환하며 자리를 이동하는 모습이 물 위에 올라오는 거품 모양과 같다고 하여 버블 정렬이라고 한다.
- 시간 복잡도 : O(n^2)
- [55, 7, 78, 12, 42]를 버블 정렬해보자(오름차순)




위의 그림들을 통하여 버블 정렬 과정을 살펴보았다. 이를 코드로 구현해보자!!
def bubble_sort(arr, N): # 정렬할 리스트, N 원소 수
# 1. n-1 번째 부터 조사를 해나갈 거야.
for i in range(len(arr)-1, 0, -1):
for j in range(i):
# 이전 요소가 이후 요소보다 크면
# 교환을 해야지 버블 소트가 되겠자
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
return arr
numbers = [9, 13, 64, 62, 3]
print(bubble_sort(numbers, 5))
카운팅 정렬 (Counting Sort)
- 항목들의 순서를 결정하기 위해 집합에 각 항목이 몇 개씩 있는지 세는 작업을 하여, 선형 시간에 정렬하는 효율적인 알고리즘
- 제한사항
- 정수나 정수로 표현할 수 있는 자료에 대해서만 적용 가능
- 각 항목의 발생 횟수를 기록하기 위해, 정수 항목으로 인덱스 되는 카운트들의 배열을 사용하기 때문
- 카운트들을 위한 충분한 공간을 할당하려면 집합 내의 가장 큰 정수를 알아야 함
- 정수나 정수로 표현할 수 있는 자료에 대해서만 적용 가능
- 시간 복잡도 : O(n+k), n은 리스트 길이, k는 정수의 최댓값
- [0,4,1,3,1,2,4,1]을 카운팅 정렬해보자
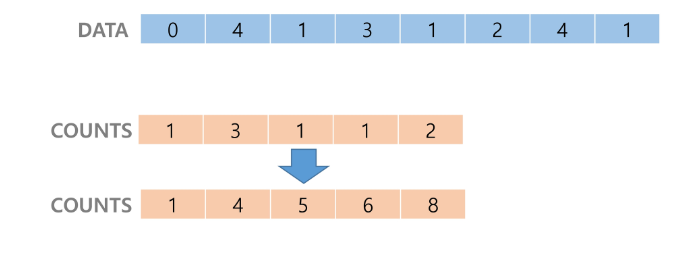
1. Data에서 각 항목들의 발생 횟수를 세고, 정수 항목들로 직접 인덱스 되는 카운트 배열 counts에 저장한다

2. 정렬된 집합에서 각 항목의 앞에 위치할 항목의 개수를 반영하기 위해 counts의 원소를 조정한다.
: 아래 그림에서 1 4 5 6 8은 0까지의 개수, 1까지의 총 개수...
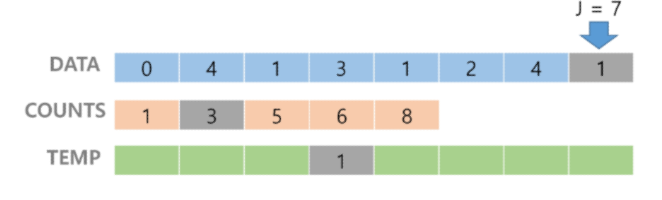
3. counts[1]을 감소시키고 Temp에 1을 삽입한다.
: 제일 끝의 수가 1이므로 counts[1]을 감소시킨다.
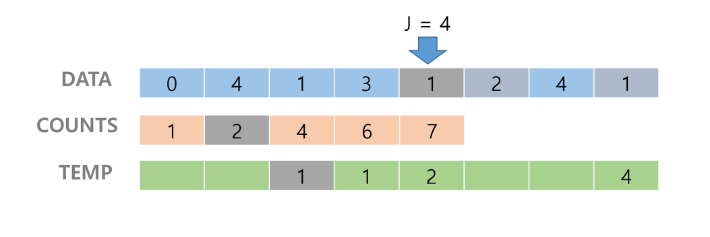
4. counts[4]를 감소시키고 temp에 1을 삽입한다.

5. counts[2]를 감소시키고 temp에 2를 삽입한다. 이런 방식으로 제일 앞에까지 간다.

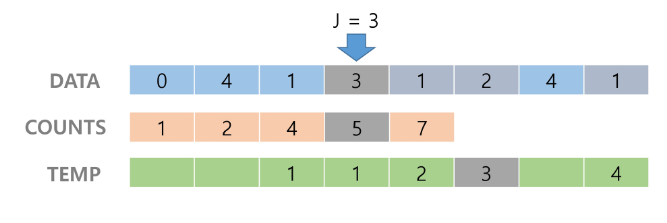

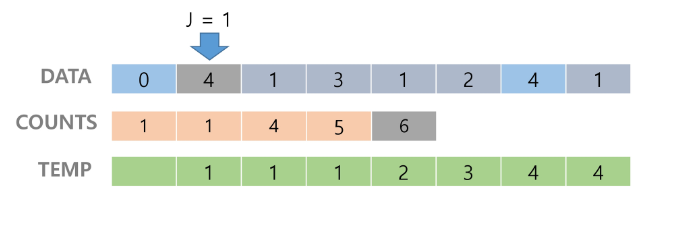

6. Temp 업데이트를 완료하고 정렬을 종료한다.
이렇게 코드로 구성해볼 수 있다.
def counting_sort(input_arr, k):
"""
input_arr : 입력 배열(1 to k)
counting_arr : 카운트 배열
k는 데이터의 개수가 아닌 데이터 원소의 범위
"""
counting_arr = [0] * (k+1)
# 1. counting array에 arr내 원소의 빈도수 담기
for i in range(0, len(input_arr)):
counting_arr[input_arr[i]] += 1
# for i in input_arr:
# counting_arr[i] += 1
# 2. 누적(counting_arr 업데이트)
for i in range(1, len(counting_arr)):
counting_arr[i] += counting_arr[i - 1]
# 3. result_arr 생성
result_arr = [-1] * len(input_arr)
# 4. result_arr에 정렬하기(counting_arr를 참조)
for i in range(len(result_arr) - 1, -1, -1):
counting_arr[input_arr[i]] -= 1
result_arr[counting_arr[input_arr[i]]] = input_arr[i]
# for i in input_arr:
# counting_arr[i] -= 1
# result_arr[counting_arr[i]] = i
return result_arr
a = [1, 4, 1, 3, 1, 2, 4, 1]
print(counting_sort(a, 4)) # [0, 1, 1, 1, 2, 3, 4, 4]
선택 정렬 (Selection Sort)
만약 포켓볼 공을 순서대로 정렬하라고 한다면 어떻게 하겠는가? 보통 가장 작은 수부터 차례로 정렬할 것이다.
이런 방법이 바로 선택 정렬이다.
뒤에서 살펴볼 셀렉션 알고리즘을 전체 자료에 적용한 것이다.
- 주어진 자료들 중 가장 작은 값의 원소부터 차례대로 선택하여 위치를 교환하는 방식
- 정렬 과정
- 주어진 리스트 중에서 최소값을 찾는다.
- 그 값을 리스트의 맨 앞에 위치한 값과 교환한다.
- 맨 처음 위치를 제외한 나머지 리스트를 대상으로 위의 과정을 반복한다.
- 미정렬원소가 하나 남은 상황에서는 마지막 우너소가 가장 큰 값을 갖게 되므로, 실행을 종료하고 선택 정렬이 완료된다.
- 시간 복잡도 : O(n2)


셀렉션 알고리즘 (Selction Algorithm)
- 저장되어 있는 자료로부터 k번재로 큰 혹은 작은 원소를 찾는 방법을 셀렉션 알고리즘이라 한다.
- 최소값, 최대값 혹은 중간값을 찾는 알고리즘을 의미하기도 한다.
- 선택 과정
- 정렬 알고리즘을 이용하여 자료 정렬하기
- 원하는 순서에 있는 원소 가져오기
- k번째로 작은 원소를 찾는 알고리즘
- 1번부터 k번째까지 작은 원소들을 찾아 배열의 앞쪽으로 이동시키고, 배열의 k번째를 반환한다.
- k가 비교적 작을 때 유용하며 O(kn)의 수행시간을 필요로 한다.

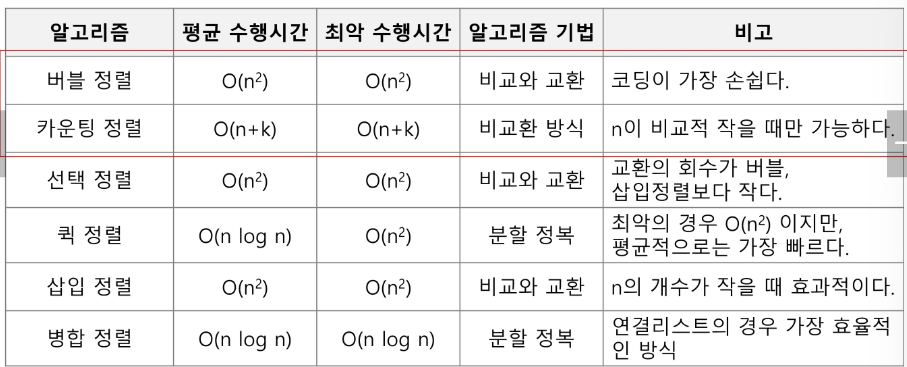
오늘 배운 정렬 알고리즘의 특성을 다른 정렬들과 비교해보며 이만 끝내자!!
728x90
'ALGORITHM > 알고리즘 알아보기' 카테고리의 다른 글
| [알고리즘] 반복문과 재귀 (1) | 2022.09.21 |
|---|---|
| [알고리즘] 정렬2 - 합병(병합), 퀵 정렬 (1) | 2022.09.09 |
| [Algorithm] 최장 증가 수열 (LIS) (0) | 2022.09.07 |
| [알고리즘] Queue를 활용한 깊이 우선 탐색(BFS) (0) | 2022.08.24 |
| [알고리즘] 분할 정복 (0) | 2022.08.22 |
