728x90
- 연속 행렬이 주어질 때, 행렬의 곱셈 중 가장 효율적인 방법을 찾는 이론
- 어떤 순서로 곱셈을 할지 결정 하는 것
- 만약, A - B - C - D 행렬이 있을 때 아래와 같은 형태로 구성될 수 있다. - 결합 법칙이 성립
(ABC)D = (AB)(CD) = A(BCD) = ...
- 곱셈 순서를 어떻게 정하는 같은 결과이므로, 가장 연산 횟수가 적은 것이 효율적일 것이다.
- 만약 A가 10 x 30, B가 30 x 5, C가 5 x 60 이면
(AB)C = (10×30×5) + (10×5×60) = 1500 + 3000 = 4500
A(BC) = (30×5×60) + (10×30×60) = 9000 + 18000 = 27000
- 따라서 아래의 점화식을 바탕으로 최적화 시킬 수 있다.

- 위의 식을 토대로 ABC의 최소 연산 회수를 구해보자.
- A : 20x1 행렬
- B : 1x30 행렬
- C : 30x10 행렬
- D : 10x10 행렬
- d0 : 20, d1 : 1, d2 : 30, d3 : 10, d4 : 10
1. M[1][2] (행렬 A~B까지의 곱의 횟수) (1<=k<=1)
= minimum(M[1][k] + M[k+1][2] + d0*dk*d2
= M[1][1] + M[2][2] + d0*d1*d2
= 0 + 0 + 20*1*30
= 600
2. M[2][3](행렬 B~C까지의 곱의 횟수) (2<=k<=2)
= minimum(M[2][k] + M[k+1][3] + d1*dk*d3)
= M[2][2] + M[3][3] + d1*d2*d3
= 0+0+1*30*10
= 300
3. M[1][3](행렬 A~C까지의 곱의 횟수)(1<=k<=2)
= minimum(M[1][k] + M[k+1][3] +d0*dk*d2
= minimum(M[1][1] + M[2][3] + d0*d1*d3, M[1][2] + M[3][3] + d0*d2*d3)
= minimum(0 + 300+20*1*10, 600+0+20*30*10)
= minimum(500, 6600)
= 500
- 행렬 A~D까지의 곱의 횟수 (M[1][4])는
- M[1][4] = minimum( M[1][1] + M[2][4] + d0*d1*d4, M[1][2] + M[3][4] + d0*d2*d4, M[1][3] + M[4][4] + d0*d3*d4)
- M[1][4]를 구하려면
- M[1][1]~M[1][4]의 값이 필요하고,(구하려는 값의 테이블 좌측값)
- M[2][4]~M[4][4]의 값이 필요하고,(구하려는 값의 테이블 아랫값)
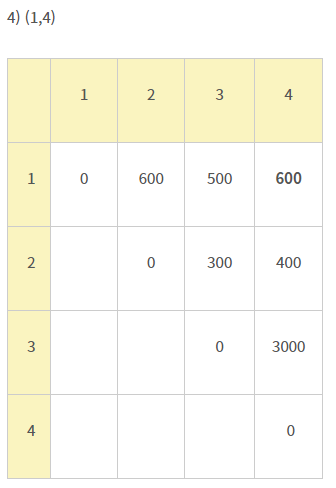
M[i][j]의 값은,
대각선을 하나씩 증가시키며 아래와 같이 구할 수 있다.



# Dynamic Programming 이용하기
import sys
def MatrixChainOrder(p, n):
m = [[0 for x in range(n)] for x in range(n)]
for i in range(1, n):
m[i][i] = 0
# L은 체인의 길이
for L in range(2, n):
for i in range(1, n-L + 1):
j = i + L-1
m[i][j] = sys.maxint
for k in range(i, j):
# q = cost / scalar multiplications
q = m[i][k] + m[k + 1][j] + p[i-1]*p[k]*p[j]
if q < m[i][j]:
m[i][j] = q
return m[1][n-1]
arr = [1, 2, 3, 4]
size = len(arr)
print("최소 연산 수는" +
str(MatrixChainOrder(arr, size)))
# This Code is contributed by Bhavya Jain
#include<iostream>
using namespace std;
#define MIN(A, B) ((A)>(B)?(B):(A))
#define MAX_VALUE 9999999
#define MAX_SIZE 101
int M[MAX_SIZE][MAX_SIZE];
int d[MAX_SIZE];
int main()
{
int size = 4;
d[0] = 20, d[1] = 1, d[2] = 30, d[3] = 10, d[4] = 10;
// 구하려는 행렬 사이즈만큼 반복한다.
for (int diagonal = 0; diagonal < size; diagonal++)
{
// i값은 상단 1부터 시작, 반복하는 횟수가 1씩 감소한다.
for (int i = 1; i <= size - diagonal; i++)
{
// j값은 우측으로 diagnonal만큼 반복할때마다 이동한다.
int j = i + diagonal;
// i와 j가 같을 경우 M[i][j] = 0
if (j == i)
{
M[i][j] = 0;
continue;
}
// k=i~j-1만큼 반복하며, 공식을 적용하여 M[i][j]에 들어갈 곱의 최소값을 구한다.
M[i][j] = MAX_VALUE;
for (int k = i; k <= j - 1; k++)
M[i][j] = MIN(M[i][j], M[i][k] + M[k + 1][j] + d[i - 1] * d[k] * d[j]);
}
}
/*결과 출력*/
cout << M[1][size] << endl;
for (int i = 1; i <= size; i++)
{
for (int j = 1; j <= size; j++)
{
cout << M[i][j] << " ";
}
cout << endl;
}
return 0;
}728x90
'ALGORITHM > 알고리즘 알아보기' 카테고리의 다른 글
| [Algorithm] 세그먼트 트리(Segment Tree) with Python (1) | 2023.05.14 |
|---|---|
| [Algorithm] CCW 알고리즘 (0) | 2023.03.19 |
| [Algorithm] 냅색 알고리즘 (Knapsack Algorithm) (0) | 2023.01.28 |
| [Algorithm] 위상정렬 (0) | 2023.01.28 |
| [Algorithm] 비트 마스크 (1) | 2023.01.22 |
