728x90
목차
- Segment Tree?
- 구현
- query 응답하기
- 업데이트
1. Segment Tree?
어떤 데이터가 존재할 때, 특정 구간의 결과값을 구하는데 사용하는 자료구조이다.
단순한 구간합 뿐만 아니라주어진 쿼리에 대해 빠르게 응답하기 위한 자료구조!!
여기서는 이해하기 쉽게 구간합을 예시로 세그먼트 트리를 알아볼 예정
아래와 같은 배열이 존재할 때, 구간합을 구해보자.

배열을 돌면서 원하는 구간의 합을 더해주면 된다!
배열의 크기가 커진다면, 시간이 더 많이 걸릴 것이다.
따라서, 구간별 합을 구해 저장해둔다면 빠르게 찾을 수 있을 것이다!!
- 세그먼트 트리는 Binary Tree(이진 트리) 구조를 가지고 있다.
- 배열의 크기
- Full Binary Tree 일 경우
- 높이는 logN
- 노드의 개수 2 * (H+1) 개
- N이 2의 제곱꼴이 아닌 경우
- 높이 H = ceil(logN) => 올림
- 배열의 크기 => 2^(H+1) -1
- Full Binary Tree 일 경우
- 배열의 크기
- 선형 탐색보다 좀 더 효율적인 탐색이 가능하다.
- 특히, 누적합의 경우 특정 데이터 변경 시 O(N)으로 업데이트
- 세그먼트 트리는 O(logN)으로 반영 => 최악의 경우 O(NlogN)
- 단점으로는 기본 완전 탐색 사용에 비해 더 많은 메모리가 필요하게 된다.

- 위에서 정의한 배열을 세그먼트 트리로 나타낸 것이다.
- 각 노드의 숫자는
- 리프노드 : 배열의 그 수 자체
- 다른 노드 : 왼쪽 자식과 오른쪽 자식의 합을 저장
- 따라서, x 번호의 노드의 왼쪽 자식 번호는 2 * x, 오른쪽 자식의 번호는 2 * x + 1이 된다.
- 계산을 편리하게 하기 위해서 0번이 아닌 1번 인덱스부터 시작하는 것이 좋다.

2. 구현
- Top-down 방식 - 재귀 이용
- 재귀를 이용하기 때문에 bottom-up 방식에 비해 접근 성과 성능은 떨어지지만, 확장성이 좋아서 lazy propagation을 사용할 때 유용하다.
- 이름의 뜻 그대로 게으르게(lazy) 전파(propagation) 한다는 것으로 특정 업데이트 구간에 포함되는 노드들에게 나중에 전파시킬 값을 저장해 둠으로써 다음 업데이트나 쿼리를 할 때 마다 자식노드들 한테만 전파해주면 되게 된다.
- 다른 포스트에서 다룰 예정
- 재귀를 이용하기 때문에 bottom-up 방식에 비해 접근 성과 성능은 떨어지지만, 확장성이 좋아서 lazy propagation을 사용할 때 유용하다.
- nums = [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ] 배열을 예시로 들어보자.
- 우선, 트리 높이와 배열의 크기를 구해준 후, 계산의 편의를 위해 0번 인덱스를 추가해주자.
from math import ceil, log
nums = [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ]
H = ceil(log(len(nums), 2))
tree_size = pow(2, H+1) - 1
segment_tree = [0] + [0] * tree_size
# segment_tree = [0] *(pow(2, ceil(log(len(nums), 2)) + 1) -1)
print(H, tree_size, len(segment_tree))- 이제 배열의 값을 segment_tree에 저장해주면서 구간 합을 기록해줄 것이다.
- 좌측 노드의 좌표 : node * 2, 구간 : left - mid
- 우측 노드의 좌표 : node * 2 + 1, 구간 : mid + 1, right
- 현재 노드의 좌표 : node, 구간 : left - right, 값 : 좌/우측 노드의 합
- 위 3개의 좌표를 사용하며 범위를 절반으로 나누며 연산을 노드에 저장해준다.
- 구간 길이가 1이라면 (left와 right가 같다면) 트리에 자기 자신을 저장하면 된다 => 리프 노드 기록하는 것
- 아래와 같은 순서로 기록된다.
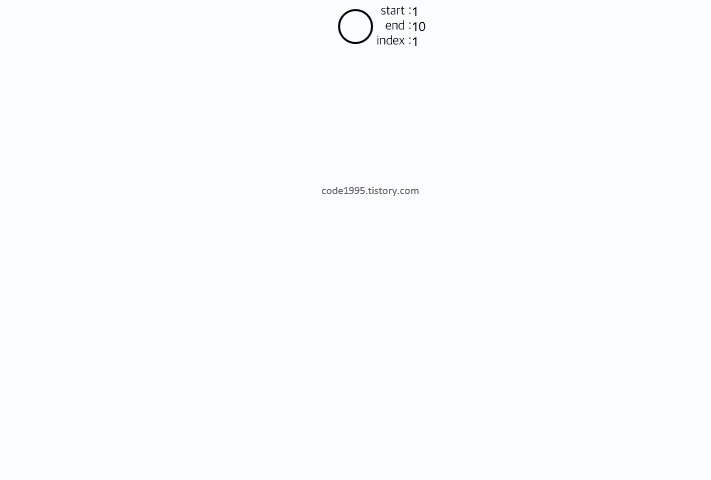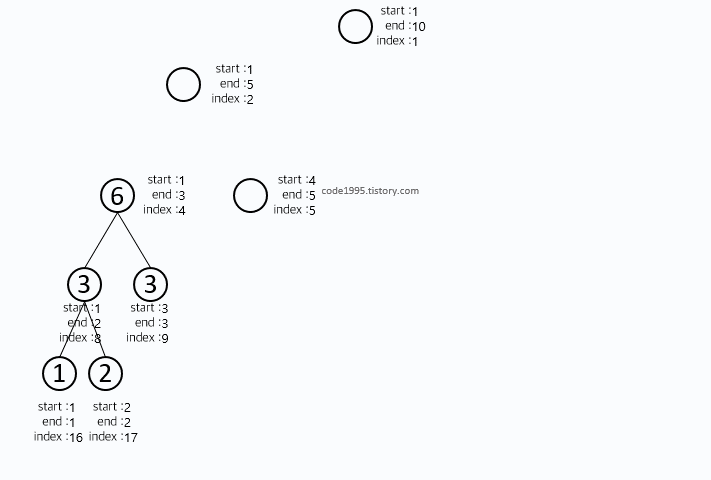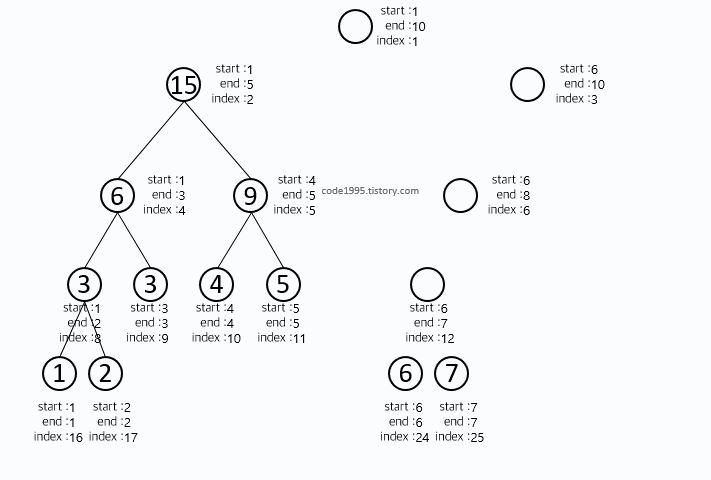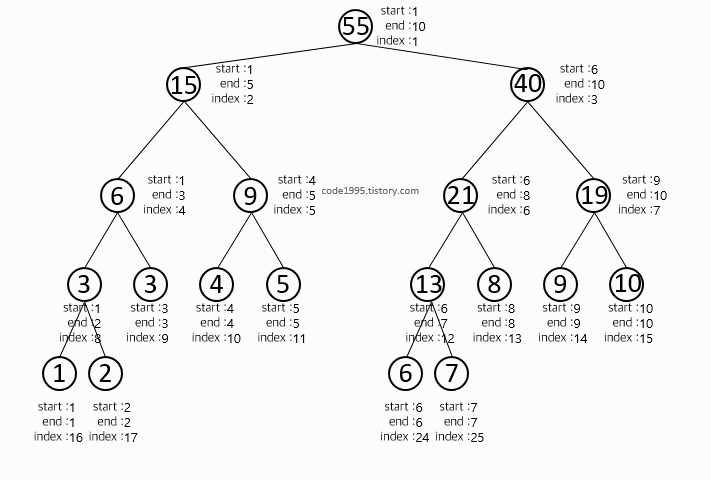
from math import ceil, log
def segment(left, right, i):
if left == right:
segment_tree[i] = nums[left]
return segment_tree[i]
mid = (right+left)//2
segment_tree[i] = segment(left, mid, i*2) + segment(mid+1, right, i*2+1)
return segment_tree[i]
nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
H = ceil(log(len(nums), 2)+1)
tree_size = pow(2, H+1) - 1
segment_tree = [0] + [0] * (pow(2, ceil(log(len(nums), 2)+1) + 1) - 1)
segment(0, len(nums)-1, 1)
print(segment_tree)
3. 쿼리에 따른 출력
- 세그먼트 트리에서 쿼리는 대부분 '범위'
- 아래와 같은 조건을 생각하며 분기를 해주면 된다.
- 구간이 노드의 구간에 완전히 벗어난 경우 -> 0 리턴
- 요청 구간이 노드의 구간을 완전히 포함한 경우 -> 트리 좌표의 값 리턴
- 노드의 구간이 요청 구간을 완전히 포함한 경우 -> 요청 구간 외의 잉여 구간 배제해야 하므로 절반씩 나눠 재귀 탐색
- 요청 구간이 노드의 구간에 걸쳐진 경우 -> 3번과 같이 더 깊이 탐색해서 요청 외 잉여 구간 배제
- start, end => 현재 노드의 포용 범위
- left, right => 쿼리로 주어진 조건을 구해야 하는 범위
def query_sum(start, end, idx, left, right):
if left > end or right < start:
return 0
if left <= start and right >= end:
return segment_tree[idx]
mid = (start + end) // 2
return query_sum(start, mid, idx*2, left, right) + query_sum(mid+1, end, idx*2+1, left, right)
print('sum 0 to 5 : ', query_sum(0, len(nums)-1, 1, 0, 5))
# sum 0 to 5 : 21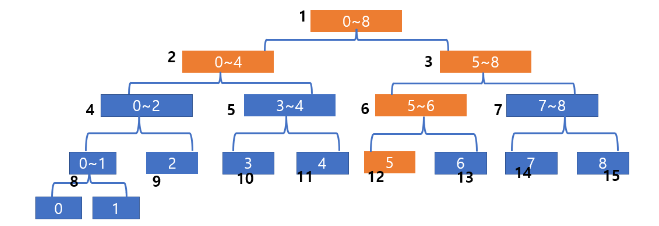
- 0~5번까지 합을 구하라는 문제를 받았을 때, 실행 예시를 보자.
- 루트 노드 (1번)은 0~8까지의 정보를 담고 있고, 우리가 구해야 되는 0~5번을 포함하면서 더 크기 때문에 절반을 나눠준다.
- 0~4는 완전 포함 되므로 return해준다.
- 5~8의 경우는 관심 구간을 포함 중이므로 다시 쪼개주고 5~6도 관심구간 포함이므로 쪼개준다.
- 이후 5를 return하면 완성된다.
4. 세그먼트 트리 업데이트
- 재귀로 업데이트
- 함수의 인자로 원래 값과의 차이만 넣어서, 루트노드부터 아래로 내려오면서 값을 업데이트 해주면 된다.
- 현재 노드의 포용구간에 업데이트 노드가 없는 경우 그대로 값 반환
- 아니라면 변경 값만큼 + 해준다.
- 리프노드가 아니라면 다시 자식 노드 탐색, 리프 노드라면 return
# 현재 노드의 포용범위 start, end
# 현재 노드 node
# 변경할 리프노드의 번호와 값 idx, val
def update(start, end, node, idx, val):
if start > idx or idx > end:
return segment_tree[node]
segment_tree[node] += val
if start != end:
mid = (start + end) // 2
update(start, mid, node*2, idx, val)
update(mid+1, end, node * 2 +1, idx, val)
print('sum 0 to 5 : ', query_sum(0, len(nums)-1, 1, 0, 5))
update(0, len(nums)-1, 1, 0, 2)
print('sum 0 to 5 : ', query_sum(0, len(nums)-1, 1, 0, 5))
print(segment_tree)
전체 코드
from math import ceil, log
def segment(left, right, i):
if left == right:
segment_tree[i] = nums[left]
return segment_tree[i]
mid = (right+left)//2
segment_tree[i] = segment(left, mid, i*2) + segment(mid+1, right, i*2+1)
return segment_tree[i]
def query_sum(start, end, idx, left, right):
if left > end or right < start:
return 0
if left <= start and right >= end:
return segment_tree[idx]
mid = (start + end) // 2
return query_sum(start, mid, idx*2, left, right) + query_sum(mid+1, end, idx*2+1, left, right)
# 현재 노드의 포용범위 start, end
# 현재 노드 node
# 변경할 리프노드의 번호와 값 idx, val
def update(start, end, node, idx, val):
if start > idx or idx > end:
return segment_tree[node]
segment_tree[node] += val
if start != end:
mid = (start + end) // 2
update(start, mid, node*2, idx, val)
update(mid+1, end, node * 2 +1, idx, val)
# sum 0 to 5 : 21
nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
H = ceil(log(len(nums), 2)+1)
tree_size = pow(2, H+1) - 1
segment_tree = [0] + [0] * (pow(2, ceil(log(len(nums), 2)) + 1) - 1)
segment(0, len(nums)-1, 1)
print('sum 0 to 5 : ', query_sum(0, len(nums)-1, 1, 0, 5))
update(0, len(nums)-1, 1, 0, 2)
print('sum 0 to 5 : ', query_sum(0, len(nums)-1, 1, 0, 5))
print(segment_tree)
https://www.acmicpc.net/problem/2042
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
- bottom-up 방식으로 해당 문제를 푸신 분 코드 이다.
- top-down에 비하여 속도에서 상당한 차이를 보여주었다.
- 시간내서 꼭 구현해 봐야 겠다
- 여기서 구간 합을 구하는 부분에 start % 2와 not end % 2인 경우에만 total에 append해주는 이유는
- 시작위치가 % 2 = 1인 경우 => 오른쪽 자식이므로 구해야 되는 값의 리프 노드라고 생각하면 된다.
- 끝나는 위치가 not % 2 = 0 => 왼쪽 자식이므로 구해야 되는 값의 리프 노드라고 생각하면 된다.
import sys
N, M, K = map(int, sys.stdin.readline().split())
def build(n):
p = 0
m = 0
while n > m:
m = 2 ** p
p += 1
tree = [0] * (m * 2)
for i in range(N):
tree[i + m] = int(sys.stdin.readline())
for i in range(m - 1, 0, -1):
tree[i] = tree[2 * i] + tree[(2 * i) + 1]
return tree, m
tree, leaf = build(N)
def change(tree, b, c, leaf):
idx = leaf + b - 1
delta = c - tree[idx] if tree[idx] < c else -(tree[idx] - c)
while idx:
tree[idx] += delta
idx //= 2
return tree
def interval_sum(tree, b, c, leaf):
total = []
start = leaf + b - 1
end = leaf + c - 1
while start < end:
if start % 2:
total.append(tree[start])
start = (start + 1) // 2
if not end % 2:
total.append(tree[end])
end = (end - 1) // 2
if start == end:
total.append(tree[start])
return sum(total)
for _ in range(M + K):
a, b, c = map(int, sys.stdin.readline().split())
if a == 1:
tree = change(tree, b, c, leaf)
else:
answer = interval_sum(tree, b, c, leaf)
print(answer)
728x90
'ALGORITHM > 알고리즘 알아보기' 카테고리의 다른 글
| [Algorithm] 이분 매칭 (Bipartite Matching) (0) | 2023.08.09 |
|---|---|
| [Algorithm] CCW 알고리즘 (0) | 2023.03.19 |
| [Algorithm] 연쇄 행렬 곱셈(Matrix Chain Multiplication) (0) | 2023.03.03 |
| [Algorithm] 냅색 알고리즘 (Knapsack Algorithm) (0) | 2023.01.28 |
| [Algorithm] 위상정렬 (0) | 2023.01.28 |
