728x90
# 백트래킹
- 해를 찾는 도중에 '막히면' (해가 아니면) 되돌아가서 다시 해를 찾아가는 기법
- 최적화(optimization) 문제와 결정(decision) 문제를 해결할 수 있다.
- 결정 : 문제의 조건을 만족하는 해가 존재하는지의 여부를 'yes' 또는 'No'가 답하는 문제
- 미로 찾기, n-Queen 문제, 부분 집합의 합 등..
정의를 보면 앞서 봤던 DFS-깊이 우선 탐색과 비슷한 것 같다. 미로 찾기 예를 통해서 어떤 차이가 있는지 알아보자.
미로 찾기
- 아래 그림과 같이 입구와 출구가 주어진 미로에서 입구부터 출구까지의 경로를 찾는 문제
- 이동할 수 있는 방향은 4가지로 제한된다.

- 내가 지나가는 경로를 스택에 저장해준 후 pop을 이용해 다시 경로를 되돌아 갈 수 있다.


# 백트래킹과 깊이우선탐색의 차이
- 어떤 노드에서 출발하는경로가 해결책으로 이어질 것 같지 않으면 더 이상 그 경로를 따라가지 않음으로써 시도의 횟수를 줄인다.(Prunning 가지치기)
- 즉, DFS의 경우 모든 경로를 추적하는데 비해 백트래킹은 불필요한 경로를 조기에 차단
- DFS를 가하기에는 경우의 수가 너무나 많다. N! 가지의 경우의 수를 가진 문제에 대해 DFS를 가하면 당연히 처리 불가능한 문제가 된다.
- 백트래킹 알고리즘을 적용하면 일반적으로 경우의 수가 줄어들지만 최악의 경우 여전히 지수함수 시간(Exponential Time)을 요하므로 처리 불가
상세 정의
- 어떤 노드의 유망성을 점검한 후에 유망(promising)하지 않다고 결정되면 그 노드의 부모로 되돌아가(backtracking) 다음 자식 노드로 감
- 어떤 노드를 방문하였을 때 그 노드를 포함한 경로가 해답이 될 수 없으면
그 노드는 유망하지 않다고 하며, 반대로 해답의 가능성이 있으면 유망 - 가지치기(pruning) : 유망하지 않는 노드가 포함되는 경로는 더 이상 고려하지 않는다.
# 과정
- 상태 공간 트리의 깊이 우선 검색을 실시한다.
- 각 노드가 유망한지를 점검
- 만일 그 노드가 유망하지 않으면, 그 노드의 부모 노드로 돌아가서 검색을 계속한다.
def checknode(v): # node
if promising(v):
if there is a solution at v:
write the
else:
for u in each child of v:
chechnode(u)

앞서 차이를 살펴본 DFS와 백트래킹을 비교해보면 DFS는 155 노드를 조사하지만, 백트래킹의 경우 27 노드만 조사한다.
또 다른 예로 부분집합 구하기와 순열을 간단하게 구해보자!
부분집합
- 어떤 집합의 공집합과 자기 자신을 포함한 모든 부분집합을 powerset이라고 하며 원소 개수가 n개 일 때 부분집합의 개수는 2^n개다.
- n개의 원소가 들어있는 집합의 2^n개의 부분집합을 만들 때는, true 또는 false값을 가지는 항목들로 구성된 n개의 배열을 만드는 방법을 이용
- 여기서 배열의 i번째 항목은 i번째의 원소가 부분집합의 값인지 아닌지를 나타내는 값
아래는 이전에 각 원소가 부분집합에 포함되었는지를 loop 이용하여 확인하고 생성하는 방법이다.
bit = [0, 0, 0, 0]
for i in range(2):
bit[0] = i
for j in range(2):
bit[1] = j
for k in range(2):
bit[2] = k
for l in range(2):
bit[3] = 1
print(bit)- powerset을 backtracking 알고리즘을 이용해 구해보자.

N = 3
arr = [1, 2, 3] # 우리가 활용할 데이터
sel = [0] * N # a리스트 (내가 해당 원소를 뽑았는지 체크)
def powerset(idx):
if idx == N:
print(sel, ":", end = ' ')
for i in range(N):
if sel[i]:
print(arr[i], end=' ')
print()
return
# idx 자리의 원소를 뽑고 간다.
sel[idx] = 1
powerset(idx+1)
# idx 자리를 안뽑고 간다.
sel[idx] = 0
powerset(idx + 1)
powerset(0)
# =>
# [1, 1, 1] : 1 2 3
# [1, 1, 0] : 1 2
# [1, 0, 1] : 1 3
# [1, 0, 0] : 1
# [0, 1, 1] : 2 3
# [0, 1, 0] : 2
# [0, 0, 1] : 3
# [0, 0, 0] :
순열
arr = [1, 2, 3]
n = 3
sel = [0] * n
check = [0] * n
# 재귀방식
def perm(idx):
# 다 뽑아서 정리했다면
if idx == n:
print(sel)
else:
for i in range(n):
if check[i] == 0:
sel[idx] = arr[i] # 값을 사용해라
check[i] = 1 # 사용을 했다는 표시
perm(idx+1)
check[i] = 0 # 다음 반복문을 위한 원상복구
perm(0)
# =>
# [1, 2, 3]
# [1, 3, 2]
# [2, 1, 3]
# [2, 3, 1]
# [3, 1, 2]
# [3, 2, 1]
# --------- #
# 비트연산 방식
# check 10진수 정수
def perm(idx, check):
if idx == n:
print(sel)
return
for i in range(n):
# i 번째 원소를 활용했군, 그럼 안쓰고 넘어가지
if check & (1<<i): continue
sel[idx] = arr[i]
perm(idx+1, check | (1<<i)) # 원상복구가 필요없다...
perm(0,0)
# => 결과는 위와 동
# ---------------- #
# 스왑 방식
def perm(idx):
if idx == n:
print(arr)
else:
for i in range(idx, n):
# 순서를 바꾸고
arr[idx], arr[i] = arr[i], arr[idx]
perm(idx + 1)
# 원상복구
arr[idx], arr[i] = arr[i], arr[idx]
perm(0)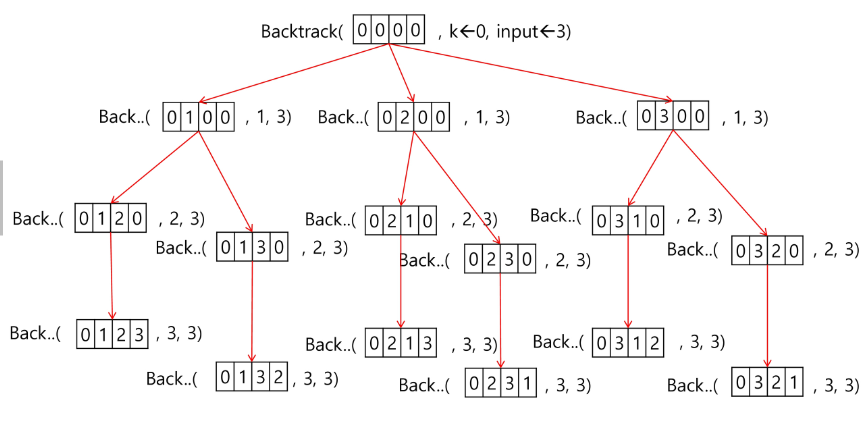
[참고] 부분집합의 합
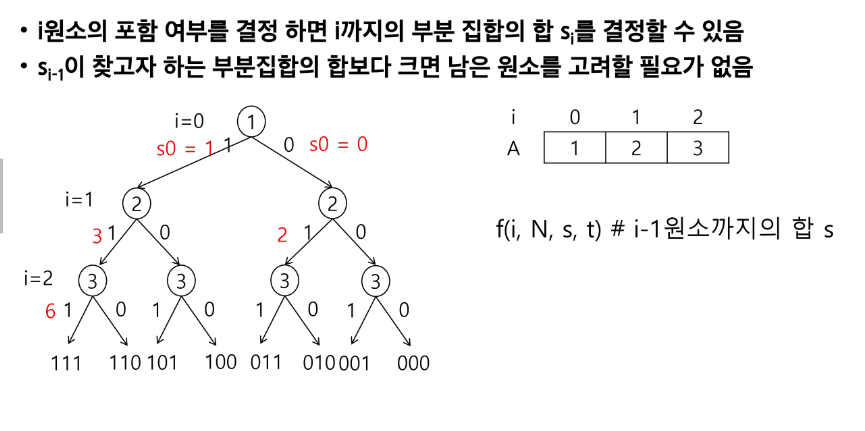
아직 너무 어렵지만 문제를 통해서 극복해보는 수밖에..
다음 글에서 분할 정복에 대해 간단히 알아보고 끝내자
728x90
'ALGORITHM > 알고리즘 알아보기' 카테고리의 다른 글
| [알고리즘] Queue를 활용한 깊이 우선 탐색(BFS) (0) | 2022.08.24 |
|---|---|
| [알고리즘] 분할 정복 (0) | 2022.08.22 |
| [알고리즘] 후위 표기법 - 계산기 (0) | 2022.08.22 |
| [알고리즘] DFS(깊이 우선 탐색) (0) | 2022.08.17 |
| [알고리즘] Memoization과 동적 프로그래밍 (0) | 2022.08.17 |
