728x90
LIFO 구조의 Stack을 이용하여 계산기를 구현해보자.
여기서의 계산기는 중위 표기법(infix notation) (A+B)를 후위 표기법(postfix notation)(AB+)으로 변경하여 스택을 이용하여 계산한다.
중위 표기식의 후위 표기식 변환 방법 1
- 수식의 각 연산자에 대해 우선순위에 따라 괄호를 사용하여 다시 표현
- 각 연산자를 그에 대응하는 오른쪽 괄호의 뒤로 이동시킨다.
- 괄호를 제거한다.

변환 알고리즘 2 (스택 이용)
- 입력받은 표기식에서 토큰을 읽는다.
- 토큰이 피연산자이면 토큰 출력
- 토큰이 괄호를 포함한 연산자일 때, 토큰이 스택의 TOP에 저장되어 있는 연산자보다 우선순위가 높으면 스택에 PUSH 하고, 그렇지 않다면 스택 top의 연산자의 우선순위가 토큰의 우선순위보다 작을 때까지 스택에서 pop 한 후 토큰 연산자를 push 한다. 만약 top에 연산자 없으면 push
- 토큰이 ')'이면 스택 top에 '('가 올 때까지 스택에 pop연산 수행하고 pop한 연산자 출력
- 더 읽을 것이 없다면 중지, 읽을 것이 있다면 1부터 다시 반복
- 스택에 남아있는 연산자를 모두 pop하여 출력
- 스택 밖의 왼 괄화는 우선순위가 가장 높지만, 스택 안의 왼쪽 괄호는 우선순위가 가장 낮다.





이렇게 후위표기법으로 바꾸는 방법을 보았다.
그럼 이제 바꾼 표기법을 가지고 계산하는 방법을 알아보자!
스택을 이용하여 계산
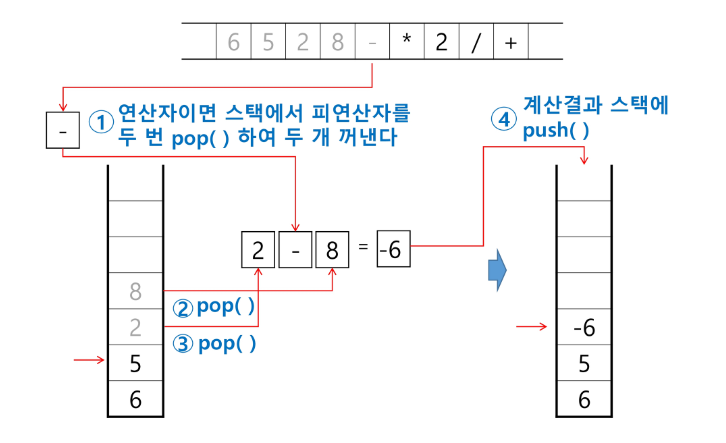
- 피연산자를 만나면 스택에 push
- 연산자를 만나면 필요한 만큼의 피연산자를 스택에서 pop 하여 연산하고, 연산 결과를 다시 스택에 push 한다.
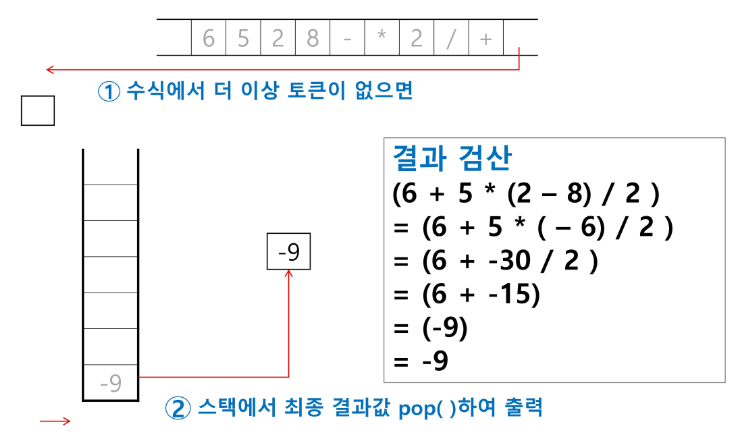
- 수식이 끝나면, 마지막으로 스택을 pop

# 후위 표기법으로 변경 코드
for t in range(1,11):
N = int(input())
tokens =list(map(str,input().rstrip())) # 입력받기
lst = [] # 빈 리스트 생성
stack = [] # 스택 생성
prior = {'*':3,'/':3,'+':2,'-':2,'(':1} # 우선순위 설정
for n in range(len(tokens)): # 토큰의 길이만큼 반복하여
if tokens[n].isdigit(): # 만약 숫자이면 바로 lst에 추가
lst.append(tokens[n])
elif tokens[n] == '(': # (이면 바로 stack에 추가
stack.append(tokens[n])
elif tokens[n] == ')': # )가 나오면 stack에서 (가 나올때까지 pop처리 및 lst에 추가.
while stack[-1] != '(':
lst.append(stack.pop())
stack.pop() # (가 나타나면 pop처리
else: # 그외에 경우 tokens[n]이 stack[-1]의 우선순위와 같거나 보다 작으면 tokens[n]의 우선순위가 더 커질때까지 pop
while stack and prior[tokens[n]] <= prior[stack[-1]]:
lst.append(stack.pop()) # pop한것들은 lst에 추가 시켜줌
stack.append(tokens[n]) # 위의 조건이 완료 되면 stack에 추가
while len(stack) != 0: # stack에 남아있는 연산자들 lst에 추가
lst.append(stack.pop())# 후위 표기법 계산
op_check = ['+','/','*','-'] # 연산자 체크를 위해 미리 생성
stack =[] # 피연산자 바로 추가할 리스트 생성
a1=0 # stack[-1]을 위한 변수 생성
a2=0 # stack[-2]을 위한 변수 생성
for l in range(len(lst)): # 후위표기법으로 저장되 있는 리스트의 수만큼 반복
if lst[l].isdigit(): # 만약 피연산자이면 바로 stack에 추가
stack.append(int(lst[l]))
elif lst[l] == '+': # + 이면 stack에서 2개 피연산자를 pop하여 게산해준뒤 다시 stack에 추가
a1 = stack.pop()
a2 = stack.pop()
stack.append(a1 + a2)
elif lst[l] == '-': # - 이면 stack에서 2개 피연산자를 pop하여 게산해준뒤 다시 stack에 추가
a1 = stack.pop()
a2 = stack.pop()
stack.append(a1 - a2)
elif lst[l] == '*': # * 이면 stack에서 2개 피연산자를 pop하여 게산해준뒤 다시 stack에 추가
a1 = stack.pop()
a2 = stack.pop()
stack.append(a1 * a2)
elif lst[l] == '/': # / 이면 stack에서 2개 피연산자를 pop하여 게산해준뒤 다시 stack에 추가
a1 = stack.pop()
a2 = stack.pop()
stack.append(a1 / a2)간단하게 스택을 이용하여서 계산하는 법을 알아보았다.
다음 글에서는 '백트래킹(Backtracking)' 기법에 대해 알아보자
728x90
'ALGORITHM > 알고리즘 알아보기' 카테고리의 다른 글
| [알고리즘] 분할 정복 (0) | 2022.08.22 |
|---|---|
| [알고리즘] 백트래킹(Backtracking) (0) | 2022.08.22 |
| [알고리즘] DFS(깊이 우선 탐색) (0) | 2022.08.17 |
| [알고리즘] Memoization과 동적 프로그래밍 (0) | 2022.08.17 |
| 알고리즘 - 검색(Search) (0) | 2022.08.10 |
