728x90
예전에 보았던 배열, 2차원 리스트와 같이 자료구조의 하나인 Stack에 대해서 알아보자.
알고리즘 문제를 풀면서도 많이 사용될 것이고 그 다음 구조, 알고리즘을 풀기 위해서는 잘 알아두는 것이 좋아보인다.
# Stack
- 물건을 쌓아 올리듯 자료를 쌓아 올린 형태의 구조
- 저장된 자료는 선형 구조를 갖는다.
- 선형구조 : 자료 간의 관계가 1ㄷ1의 관계를 갖는다.
- 비선형구조: 자료 간의 관계가 1대 N의 관계를 갖는다 (예: 트리)
- 스택에 자료를 삽입하거나 자료를 꺼낼 수 있다.
- 마지막에 삽입한 자룔르 가장 먼저 꺼낸다. 즉 후입선출(LIFO, Last in First Out) 구조를 갖는다.
스택 구현 위하여 필요한 자료구조와 연산
- 자료구조: 자료를 선형으로 저장할 저장소
- 배열 사용 가능
- 저장소 자체를 스택이라 부름
- 마지막 삽입된 원소 위치를 top이라 부름
- 연산
- 삽입 : 저장소에 자료 저장 -> push라 부른다.
- 삭제 : 저장소에서 자료 꺼냄 -> 삽입 자료의 역순으로 꺼냄 -> pop이라 부름
- 스택이 공백인지 아닌지 확인하는 연산 -> isEmpty
- 스택의 top에 있는 item(원소)을 반환하는 연산 -> peek
삽입/삭제 과정
- 빈 스택에 원소 A,B,C를 차례로 삽입 후 한번 삭제하는 연산과정

삽입과 삭제하는 것을 Push와 Pop이라고 부른다고 하였다.
코드에서는 어떻게 구현을 할까?
push 알고리즘
def push(item):
s.append(item)
pop 알고리즘
def pop() :
if len(s) == 0:
#underflow
return
else:
return s.pop(-1);
# 스택 클래스 구현
# class 베이스 스택 구현
class Stack:
# stack이 최초 생성 될때 필요한 정보들
# 생성자에 담을건데
# stack이라는 자료형은 최대 크기가 지정
def __init__(self, size):
# stack의 크기
self.size = size
# stack에 자료를 저장할 구조
# stack 처음 만들어질 때, 각 요소들은 값이 없어야 한다.
self.arr = [None] * size # 0 X None O
# stack의 최상단
self.top = -1
# stack이 비어있는지 확인하는 메서드
def is_empty(self):
if self.top == -1:
return True
else:
return False
# stack이 가득 찼는지 확인하는 메서드
def is_full(self):
if self.top + 1 == self.size:
return True
else:
return False
# stack에 값을 추가 하는 연산
def push(self, item):
if self.is_full():
raise Exception('stack이 가득 찼습니다.')
else:
self.top += 1
self.arr[self.top] = item
# stack에 값을 제거 하는 연산
def pop(self):
if self.is_empty():
raise Exception('stack이 비었습니다')
else:
value = self.arr[self.top]
self.arr[self.top] = None
self.top -= 1
return value
스택 구현시 고려사항
- 1차원 배열을 사용하여 구현할 경우 구현이 용이하다는 장점이 있지만 스택의 크기를 변경하기 어렵다
- 이를 해결하기 위해 저장소를 동적으로 할당하여 스택을 구현하는 방법이 있다. 즉, 동적 리스트를 이용하여 구현하는 방법을 의미
- 구현이 복잡하다는 단점이 있지만 메모리를 효율적으로 사용한다는 장점
스택 응용
1. 괄호 검사
- 왼쪽 괄호의 개수와 오른쪽 괄호의 개수가 같아야 한다.
- 같은 괄호에서 왼쪽 괄호는 오른쪽 괄호보다 먼저 나와야 한다.

- 문자열에 있는 괄호를 차례대로 조사하면서 왼쪽 괄호를 만나면 스택에 삽입, 오른쪽 괄호를 만나면 스택에서 top괄호를 삭제한 후 짝이 맞는지를 검사하면 된다. 프로그램을 작성해보고 직접 검사해보자!
# class 베이스 스택 구현
class Stack:
# stack이 최초 생성 될때 필요한 정보들
# 생성자에 담을건데
# stack이라는 자료형은 최대 크기가 지정
def __init__(self, size):
# stack의 크기
self.size = size
# stack에 자료를 저장할 구조
# stack 처음 만들어질 때, 각 요소들은 값이 없어야 한다.
self.arr = [None] * size # 0 X None O
# stack의 최상단
self.top = -1
# stack이 비어있는지 확인하는 메서드
def is_empty(self):
if self.top == -1:
return True
else:
return False
# stack이 가득 찼는지 확인하는 메서드
def is_full(self):
if self.top + 1 == self.size:
return True
else:
return False
# stack에 값을 추가 하는 연산
def push(self, item):
if self.is_full():
raise Exception('stack이 가득 찼습니다.')
else:
self.top += 1
self.arr[self.top] = item
# stack에 값을 제거 하는 연산
def pop(self):
if self.is_empty():
raise Exception('stack이 비었습니다')
else:
value = self.arr[self.top]
self.arr[self.top] = None
self.top -= 1
return value
# 전체 테스트 케이스
T = int(input())
for tc in range(1, T+1):
gwalho = input()
stc = Stack(len(gwalho))
if gwalho[0] == ')':
print(f'{tc} -1')
else:
for i in gwalho:
if i == '(':
stc.push(i)
else:
stc.pop()
if stc.is_empty():
print(f'{tc} 1')
else:
print(f'{tc} -1')
2. Function call
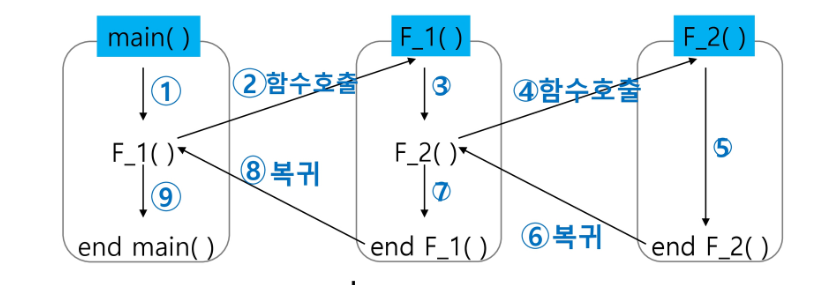
- 프로그램에서의 함수 호출과 복귀에 따른 수행 순서를 관리
- 가장 마지막 호출 함수가 가장 먼저 실행 완료 후 복귀하는 후입선출 구조, 따라서 스택을 이용하여 수행순서 관리
- 호출이 발생하면 호출한 함수 수행에 필요한 지역변수, 매개변수 및 수행 후 복귀할 주소 등의 정보를 스택 프레임(stack frame)에 저장하여 시스템 스택에 난입
- 실행이 끝나면 스택의 top 원소(스택 프레임)를 삭제하면서 복귀주소를 확인하고 복귀
- 함수 호출과 복귀에 따라 이 과정을 반복하여 전체 프로그램 수행이 종료되면 시스템 스택은 공백이 된다.
# 재귀 호출
- 자기 자신을 호출하여 순환 수행 되는 것
- 함수에서 실행해야 하는 작업의 특성에 따라 일반적인 호출방식보다 재귀호출방식을 사용하여 함수를 만들면 프로그램의 크기를 줄이고 간단하게 작성
factorial
- n에 대한 factorial : 1부터 n까지의 모든 자연수를 곱하여 구하는 연산
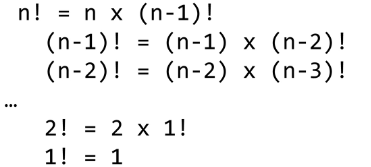
- 마지막에 구한 하위 값을 이용하여 상위 값을 구하는 작업을 반복한다.
# n=4인 경우의 실행
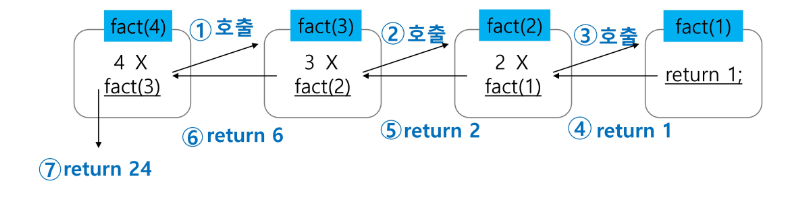
피보나치 수열
- 0과 1로 시작하고 이전의 두 수 합을 다음 항으로 하는 수열을 피보나치라 한다.
- 0, 1, 1, 2, 3, 5, 8, ...
- 피보나치 수열의 i번 째 값을 계산하는 함수 F를 정의해보자
- F(0) = 0, F(1) = 1
- F(i) = F(i-1) + F(i-2) for i >= 2
- 이 함수 F의 정으로부터 피보나치 수열의 i번째 항을 반환하는 함수를 재귀함수로 구현할 수 있다.
def fibo(n):
if n < 2 :
return n
else:
return fibo(n-1) + fibo(n-2)
과연 재귀함수로 이를 구현하는 것이 최선일까? 다음 글에서 Memoization과 동적 프로그래밍에 대해 알아보자.
728x90
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 큐(Queue)활용 - 버퍼(Buffer), deque with Python (0) | 2022.09.09 |
|---|---|
| [자료구조] 큐(Queue) - 선형 큐, 원형 큐, 우선순위 큐 with Python (0) | 2022.09.09 |
| [자료구조]- 문자열 (자료형) (1) | 2022.09.09 |
| [자료구조] 2차원 배열 with Python (0) | 2022.09.09 |
| [자료구조] 배열과 리스트 with Python (0) | 2022.09.09 |
