728x90
이분 탐색(Binary Search) 문제들 중 최적화를 위해 결정 문제로 바꿔서 푸는 매개 변수 탐색 문제가 있다.
앞에서 많이 살펴 봤지만 이분 탐색에 대해 간단히 복습해보자.
목차
- 이분 탐색
- LOWER, UPPER BOUND
- 매개변수 탐색
1. 이분 탐색
- 정렬된 배열에서 사용 가능한 알고리즘
- 시작, 끝, 중간점을 이용해 탐색 범위를 절반씩 좁혀가며 탐색한다.
- target data와 middle data 값을 반복적으로 비교하여 원하는 데이터를 찾는다.
- 예 - 4를 찾는 과정



# 재귀 이용
def binary_search(array, target, start, end):
if start > end:
return None
mid = (start + end) // 2
if array[mid] == target:
return mid
elif array[mid] > target:
return binary_search(array, target, start, mid - 1)
elif array[mid] < target:
return binary_search(array, target, mid + 1, end)
n, target = map(int, input().split())
array = list(map(int, input().split()))
result = binary_search(array, target, 0, n - 1)
if result is None:
print("원소가 존재하지 않습니다.")
else:
print(result + 1)
# 반복문 구현
def binary_search(array, target, start, end):
while start <= end:
mid = (start + end) // 2
if array[mid] == target:
return mid
elif array[mid] > target:
end = mid - 1
else:
start = mid + 1
return None
n, target = map(int, input().split())
array = list(map(int, input().split()))
result = binary_search(array, target, 0, n - 1)
if result is None:
print("원소가 존재하지 않습니다.")
else:
print(result + 1)
2. Lower, Upper Bound
Lower Bound
- Lower bound는 데이터 내에서 특정 값보다 같거나 큰 값이 처음 나오는 위치를 리턴해준다.
- 따라서, 이분 탐색의 시작점 = lo를 기준으로 리턴
def lower_bound(data, target):
lo = 0
hi = len(data)
while lo < hi:
mid = (lo + hi) // 2
if target <= data[mid]:
hi = mid
else:
lo = mid + 1
return lo
- python에서는 bisect_left 함수를 이용할 수 있다.
## bisect_left 사용 예시
import bisect
x = int(input())
arr = list(map(int, input().split()))
# dp 리스트, 시작은 배열의 0번 인덱스로 시작
dp = [arr[0]]
for i in range(x):
if arr[i] > dp[-1]:
dp.append(arr[i])
else:
# bisect이용하여 들어갈 왼쪽 인덱스 구해주기
# 1, 2, 6이 들어가있는데 현재수가 5라면
# 6의 인덱스 왼쪽 2를 반환해준다.
idx = bisect.bisect_left(dp, arr[i])
dp[idx] = arr[i]
### bisect_left 함수 내부
def bisect_left(a, x, lo=0, hi=None):
if lo < 0:
raise ValueError('lo must be non-negative')
if hi is None:
hi = len(a)
while lo < hi:
mid = (lo+hi)//2
# Use __lt__ to match the logic in list.sort() and in heapq
if a[mid] < x: lo = mid+1
else: hi = mid
return lo
Upper Bound
- Upper Bound는 특정 값보다 처음으로 큰 값이 나오는 위치를 리턴해준다.
- 마찬가지로 bisect_right 함수 사용가능
def upper_bound(data, target):
lo = 0
hi = len(data)
while lo < hi:
mid = (lo + hi) // 2
if target >= data[mid]:
lo = mid + 1
else:
hi = mid
return lo
arr=[50, 80, 81, 150, 150, 150, 150, 210, 260]
target=150
lower_bound = 3
upper_bound = 7def bisect_right(a, x, lo=0, hi=None):
if lo < 0:
raise ValueError('lo must be non-negative')
if hi is None:
hi = len(a)
while lo < hi:
mid = (lo+hi)//2
# Use __lt__ to match the logic in list.sort() and in heapq
if x < a[mid]: hi = mid
else: lo = mid+1
return lo
3. 매개 변수 탐색
- 최적화 문제 : 어떤 알고리즘의 최적의 솔루션을 찾아내는 것
- 결정 문제 : 답이 이미 결정되어 있다고 보고 문제를 푸는 것 (징검다리 문제)
최댓값, 최소값 찾기 문제
- 어떤 시점까지는 조건을 만족하지만, 그 시점 이후로는 조건을 만족하지 않는 경우에서 찾아준다.
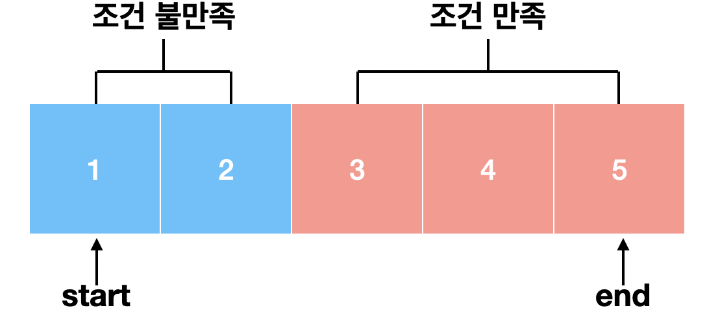
동작과정
- 문제에서 최종적으로 찾고자하는 최솟값 / 최댓값을 매개 변수로 본다.
- 결정 함수를 정의하고 구현했을 때 결과 배열이 연속인지 확인
- 최솟값이면 결정함수의 결과가 ```[f,f,.......t,t]``` 에서 f->t로 바뀌는 부분을 찾는다.
- 최댓값이면 반대
매개 변수 구간 정의
def binary_search(arr,lo,hi,value):
while lo + 1 < hi:
mid = (lo + hi) // 2
if arr[mid] <= value:
lo = mid
else:
hi = mid
return arr[lo]
- 조건 lo + 1 < hi 반복문 내에서 arr[lo] < arr[hi]가 항상 성립한다.
- lo와 hi가 1씩 차이가 날 경우 (hi-lo == 1)
- mid <=hi 또는 lo <= mid 가 되어 arr[lo] < arr[hi]가 성립하지 않을 수 있지만
- lo와 hi가 1이상 차이 날 경우 (hi-lo > 1)
- arr[lo] < arr[hi] 식은 불변식이 된다.
- 값을 찾는 조건에 따라 lo 또는 hi가 정답이 된다
- 조건 arr[mid] <= value 일 경우, arr[lo] == value 이다.
- 조건 arr[mid] < value 일 경우, arr[hi] == value 이다.
- lo, hi 구간을 정의
- lo = 구간의 최솟값 -1 & hi = 구간의 최댓값
- lo = 구간의 최솟값 으로 정의할 경우, hi는 구간의 최솟값이 될 수 없다.
(lo + 1 < hi)
결정 함수 구현
def fn(param):
pass
def binary_search(arr,lo,hi,value):
while lo + 1 < hi:
mid = (lo + hi) // 2
if fn(mid):
lo = mid # 참이면 오른쪽 구간을 탐색
else:
hi = mid # 거짓이면 왼쪽 구간을 탐색
return arr[lo]- fn(param) :
- param이 어떤 조건을 만족하면 true를 반환하고 아니면 false를 반환하게끔 구현한다.
- param은 일반적으로 문제에서 최종적으로 구해야 하는 최솟값/최댓값이 찾아야 하는 매개변수이다.
- param의 범위는 연속적이여야 한다.
- [lo, hi] 사이의 값
- fn(param)의 범위도 연속적이여야 한다.
- [false, false, ..., false, true, ..., true, true] 또는 [true, true, ..., true, false, ..., false, false]
- 중간에 false -> true 또는 true -> false 로 바뀌는 부분은 1번만 존재해야 한다.
- 만약 여러개 있을 경우, 삼분 탐색 등의 다른 방법으로 해결해야 한다.
- param의 범위는 연속적이여야 한다.
- 첫 줄의 어떤 조건이란, param 이상/이하일 때 M개의 그룹으로 나눌 수 있는가 또는 M개로 분할할 수 있는가 등을 묻는 것
728x90
'ALGORITHM > 알고리즘 알아보기' 카테고리의 다른 글
| [Algorithm] 벨만-포드 알고리즘 (0) | 2022.12.07 |
|---|---|
| [Algorithm] 투 포인터 (Two Pointer) (0) | 2022.12.03 |
| [알고리즘] 최소 신장 트리 (1) | 2022.09.29 |
| [알고리즘] 다익스트라 알고리즘 (1) | 2022.09.23 |
| [알고리즘] 반복문과 재귀 (1) | 2022.09.21 |
