728x90
시간 제한 2초, 메모리 제한 512MB
# 조건
- 사다리 게임은 N개의 세로선과 M개의 가로선으로 이루어져 있다.
- 인접한 세로선 사이에는 가로선을 놓을 수 있는데, 각각의 세로선마다 가로선을 놓을 수 있는 위치의 개수는 H이고, 모든 세로선이 같은 위치를 갖는다.
- 아래 그림은 N = 5, H = 6 인 경우의 그림이고, 가로선은 없다.

- 초록선은 세로선을 나타내고, 초록선과 점선이 교차하는 점은 가로선을 놓을 수 있는 점이다.
- 가로선은 인접한 두 세로선을 연결해야 한다.
- 단, 두 가로선이 연속하거나 서로 접하면 안 된다.
- 또, 가로선은 점선 위에 있어야 한다.

- 위의 그림에는 가로선이 총 5개 있다.
- 가로선은 위의 그림과 같이 인접한 두 세로선을 연결해야 하고, 가로선을 놓을 수 있는 위치를 연결해야 한다.
- 사다리 게임은 각각의 세로선마다 게임을 진행하고, 세로선의 가장 위에서부터 아래 방향으로 내려가야 한다.
- 이때, 가로선을 만나면 가로선을 이용해 옆 세로선으로 이동한 다음, 이동한 세로선에서 아래 방향으로 이동해야 한다.
- 위의 그림에서 1번은 3번으로, 2번은 2번으로, 3번은 5번으로, 4번은 1번으로, 5번은 4번으로 도착하게 된다.
- 아래 두 그림은 1번과 2번이 어떻게 이동했는지 나타내는 그림이다.

- 사다리에 가로선을 추가해서, 사다리 게임의 결과를 조작하려고 한다.
- 이때, i번 세로선의 결과가 i번이 나와야 한다.
- 그렇게 하기 위해서 추가해야 하는 가로선 개수의 최솟값을 구하는 프로그램을 작성하시오.
입력
- 첫째 줄에 세로선의 개수 N, 가로선의 개수 M, 세로선마다 가로선을 놓을 수 있는 위치의 개수 H가 주어진다. (2 ≤ N ≤ 10, 1 ≤ H ≤ 30, 0 ≤ M ≤ (N-1)×H)
- 둘째 줄부터 M개의 줄에는 가로선의 정보가 한 줄에 하나씩 주어진다.
- 가로선의 정보는 두 정수 a과 b로 나타낸다. (1 ≤ a ≤ H, 1 ≤ b ≤ N-1)
- b번 세로선과 b+1번 세로선을 a번 점선 위치에서 연결했다는 의미이다.
- 가장 위에 있는 점선의 번호는 1번이고, 아래로 내려갈 때마다 1이 증가한다.
- 세로선은 가장 왼쪽에 있는 것의 번호가 1번이고, 오른쪽으로 갈 때마다 1이 증가한다.
- 입력으로 주어지는 가로선이 서로 연속하는 경우는 없다.
출력
- i번 세로선의 결과가 i번이 나오도록 사다리 게임을 조작하려면, 추가해야 하는 가로선 개수의 최솟값을 출력한다.
- 만약, 정답이 3보다 큰 값이면 -1을 출력한다.
- 또, 불가능한 경우에도 -1을 출력한다.
# 접근 방법
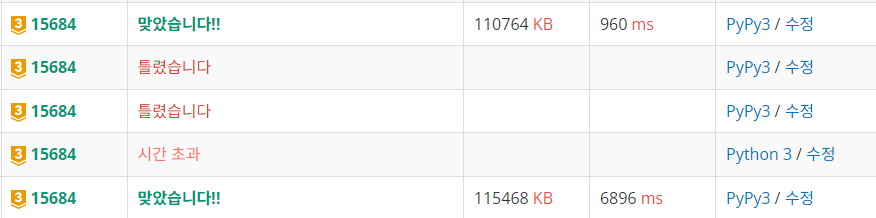
- 완전 무식하게 pypy로 통과하였다.
- 주어진 사다리의 세로 선을 배열의 한 칸으로 사용, 가로선 또한 한칸으로 사용하였다.
- 따라서 주어지는 입력값의 2N-1과 H+1을 범위로 해주었다.
- 1, 1 칸에 가로 선을 놓는다면 1번째 줄에서 0 -> 2번 열로 이동할 수 있다는 뜻..!
- 이후 조합을 사용하여 놓을 수 있는 모든 가로 칸 수를 놓아주며 Check 함수를 실행해주었다.
- 사다리에서 내려올 때는 양쪽을 확인하고 가로선이 존재한다면 dj * 2만큼 nj를 이동시켜준 후, 바로 한칸 내려온다.
- 가로선이 없다면 그냥 한 칸 내려온 후
- 만약 H+1에 도착했다면 => 도착지
- 이 때, sj가 출발지 j와 같다면 다음 탐색
- 다르다면 -1을 return한다.
- 또한 0개~3개로 탐색하므로
- 중간에 조작된 사다리를 만들 수 있다면 바로 종료해준다.
import sys
input = sys.stdin.readline
from itertools import combinations
def check():
for j in range(0, 2*N-1, 2):
si, sj = 0, j
while si <= H:
ni, nj = si, sj
for dj in [-1,1]:
if 0<=nj+dj<2*N-1:
if ladder[ni][nj+dj]:
nj += dj * 2
si, sj = ni+1, nj
break
else:
si, sj = ni+1, nj
if not sj == j:
return -1
return 0
def backtracking():
for i in range(1, 4):
for comb in combinations(can_ladder, i):
for ci, cj in comb:
if cj > 0:
if ladder[ci][cj-2]:
break
ladder[ci][cj] = 1
else:
val = check()
if not val == -1:
return i
for ci, cj in comb:
ladder[ci][cj] = 0
return -1
N, M, H = map(int, input().split())
ladder = [[0] * (2*N-1) for _ in range(H+2)]
can_ladder = []
for _ in range(M):
a, b = map(int, input().split())
ladder[a][2*b-1] = 1
for i in range(1, H+1):
for j in range(1, 2*N-1, 2):
if not ladder[i][j]:
can_ladder.append((i, j))
# 처음 주어진대로 실행하기
result = check()
if result == 0:
print(result)
else:
val = backtracking()
if not val == -1:
print(val)
else:
print(result)- 다만 pypy로도 많은 시간이 걸려 조금 더 효율적으로 고쳐보았다.
- 중점적으로 코드를 리팩토링 한 부분은 사다리의 크기와, 백트래킹하는 부분이다.
- 생각해보니 주어진 N크기만큼, H를 위 아래로 한 행씩 추가해준 후, 현재 위치에서 이어지는 사다리가 있다면 직전열에는 + 1, 현재 열 위치는 -1을 해주면서 바로 이동할 수 있게 해주었다.
- 이후, 사다리를 추가해주는 경우에도 같은 행 다음 열에 사다리가 존재한다면 추가해주지 않았다.
- 이후 백트래킹하는 부분에서 사다리를 내려오기전, 현재 comb에 연속된 가로 선이 있다면 continue를 해주었다.
- 훨씬 코드도 간결해지고 스스로 디버깅도 쉬웠지만, python으로는 아직 TL을 받게 되었다.. 아마 사다리를 움직이는 부분에서 더 효율적인 부분이 있을 거라 생각되지만.. 기록해두었다가 다음에 시도해보기로..!
import sys
input = sys.stdin.readline
from itertools import combinations
def check():
for j in range(N):
si, sj = 0, j
while si <= H:
if ladder[si][sj]:
si, sj = si+1, sj + ladder[si][sj]
else:
si, sj = si+1, sj
if not sj == j:
return -1
return 0
def backtracking():
for i in range(1, 4):
for comb in combinations(can_ladder, i):
flag = True
for c in range(1, len(comb)):
if comb[c-1] == (comb[c][0], comb[c][1]-1):
flag = False
if not flag:
continue
for ci, cj in comb:
ladder[ci][cj] = 1
ladder[ci][cj+1] = -1
else:
val = check()
if not val == -1:
return i
for ci, cj in comb:
ladder[ci][cj] = 0
ladder[ci][cj+1] = 0
return -1
N, M, H = map(int, input().split())
ladder = [[0] * N for _ in range(H+2)]
can_ladder = []
for _ in range(M):
a, b = map(int, input().split())
ladder[a][b-1] = 1
ladder[a][b] = -1
for i in range(1, H+1):
for j in range(0,N-1):
if not ladder[i][j] and not ladder[i][j+1]:
can_ladder.append((i, j))
val = check()
if not val == -1:
print(val)
else:
val = backtracking()
print(val)
728x90
'ALGORITHM > 백트래킹' 카테고리의 다른 글
| [백준 16198번] 파이썬 - 에너지 모으기 (0) | 2024.01.04 |
|---|---|
| [백준 19949번] 파이썬 - 영재의 시험 (0) | 2023.10.25 |
| [백준 6987번] 파이썬 - 월드컵 (0) | 2023.09.12 |
| [백준 14889번] 파이썬 - 스타트와 링크 (0) | 2023.09.10 |
| [백준 1342번] 파이썬 - 행운의 문자열 (0) | 2023.08.30 |
