728x90
http://www.acmicpc.net/problem/11404
11404번: 플로이드
첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가
www.acmicpc.net
# 조건
- n(2<=n<=100) 개의 도시가 있다.
- 한 도시에서 출발하여 다른 도시에 도착하는 m(1<=m<=100,000)개의 버스
- 모든 도시의 쌍 (A,B)에 대해 A에서 B로 가는데 필요한 비용의 최솟값을 구하여라
- 첫째 줄에 도시의 개수 n이 주어지고
- 둘째 줄에는 버스의 개수 m이 주어진다.
- 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다.
- 먼저 처음에는 그 버스의 출발 도시의 번호가 주어진다.
- 버스의 정보는 버스의 시작 도시 a,
- 도착 도시 b,
- 한 번 타는데 필요한 비용 c로 이루어져 있다. 시작 도시와 도착 도시가 같은 경우는 없다. 비용은 100,000보다 작거나 같은 자연수이다.
- 시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있다.
# 접근 방법
최단 거리의 경우 3 가지 방법이 존재하지만
음의 가중치가 없는 경우 벨만-포드는 사용하지 않는다.
- 다익스트라를 이용해주면 될 것 같다.
- 최단 거리를 저장해주기 위한 inf 로 가득찬 배열을 만들어 준 후, heapq를 이용해준다.
- 이미 최소비용을 넘어섰다면 continue를 통해 시간을 줄여준다.
- heapq를 이용하기 때문에 해당 도시까지 최소의 비용으로 갈 수 있다.
- 따라서 따로 방문배열을 해주지 않아도, 최단 경로를 구할 수 있음
-> 11779번 최소비용 2문제와 비슷하여 금방 풀 수 있었다.
import sys
input = sys.stdin.readline
from heapq import heappop, heappush
def route(start):
global result, dist
# 결과값 크게 잡아주기
dist = [float('inf')] * (n + 1)
# 비용, 출발점 경로 넣기
q = [(0, start)]
while q:
cost, bus_stop = heappop(q)
for next_cost, next_stop in way[bus_stop]:
if cost + next_cost >= dist[next_stop]:
continue
dist[next_stop] = cost + next_cost
heappush(q, (next_cost + cost, next_stop))
return dist
n = int(input())
m = int(input())
way = [[] for _ in range(n + 1)]
for _ in range(m):
a, b, c, = map(int, input().split())
# 비용 먼저 넣어주기
heappush(way[a], (c, b))
for i in range(1, n+1):
route(i)
dist[i] = 0
for i in range(1,n+1):
if dist[i] == float('inf'):
print(0)
else:
print(dist[i])- 플로이드-워셜 이용해주기
- 도시의 수가 100개로 많지않으므로 O(V^3)의 시간복잡도라고 해도 1,000,000번의 연산이므로 제한시간 내에 충분히 풀수 있고
- 다익스트라보다 간선의 수에 영향을 많지 않으므로 이번 문제의 경우 더 빠른 시간내에 풀 수 있다.
import sys
sys.stdin = open('input.txt')
input = sys.stdin.readline
INF = sys.maxsize
def Floyd_Warshall():
# 경유지 k
for k in range(n):
# 출발지 i
for i in range(n):
for j in range(n): # 도착지 j
if table[i][j] > table[i][k] + table[k][j]:
table[i][j] = table[i][k] + table[k][j]
return table
n = int(input())
m = int(input())
table = [[INF]*n for _ in range(n)]
for _ in range(m):
a, b, c = map(int, input().split())
if table[a-1][b-1] > c:
table[a-1][b-1] = c
for i in range(n):
table[i][i] = 0
dist = Floyd_Warshall()
for i in range(n):
for j in range(n):
if dist[i][j] == INF:
print(0, end=' ')
else:
print(dist[i][j], end=' ')
print()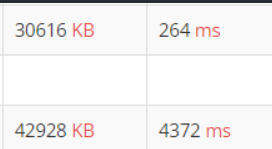
- 더 짧은 264ms가 플로이드-워셜 알고리즘 사용 코드이다.
- 플로이드의 시간 복잡도 -> O(100^3)이지만
- 다익스트라의 경우 -> O(100,000log100) 을 노드 수 만큼 해주어야 하므로 20배 정도의 차이가 나는 것 같다.
728x90
'ALGORITHM > 다익스트라, 벨만포드, 플로이드워셜' 카테고리의 다른 글
| [백준 14938번] 파이썬 - 서강 그라운드 (0) | 2022.12.29 |
|---|---|
| [백준 1956번] 파이썬 - 운동 (1) | 2022.12.27 |
| [백준 11719번] 파이썬 - 최소 비용 구하기 2 (0) | 2022.12.17 |
| [백준 1865번] 파이썬 - 웜홀 (0) | 2022.12.15 |
| [백준 1916번] 파이썬 - 최소비용 구하기 (0) | 2022.12.07 |
