728x90
GCD (최대공약수) 를 구하는 유클리드 알고리즘은 아래 게시글에서 볼 수 있다.
2022.12.09 - [ALGORITHM/알고리즘 알아보기] - [Algorithm] 유클리드 호제법 (최대 공약수, 최소 공배수)
[Algorithm] 유클리드 호제법 (최대 공약수, 최소 공배수)
최대 공약수 숫자 a,b가 주어졌을 때, 공통되는 약수 중 최대 값을 의미한다. 구하는 방법 a,b 각각의 약수를 구해서 공통되는 약수 중 가장 큰 값을 찾는 방법 찾지 않아도 되는 약수들까지 구해
cheon2308.tistory.com
이번에는, 여기서 확장된 확장 유클리드 알고리즘에 대해서 알아보자.
확장 유클리드 알고리즘을 알기 전에 배주 항등식 (Bezout's Identity)를 먼저 알아야 한다.
- 확장 유클리드 호제법이 배주 항등식의 명제를 가정으로 하여 해를 구하기 때문
배주 항등식
- GCD(a, b) = d라고 할 때,
- ax + by = d 를 만족하는 정수 x,y가 존재한다.
- d는 정수 x,y에 대하여 ax + by로 표현할 수 있는 가장 작은 정수이다.
- ax + by로 표현될 수 있는 모든 정수는 d의 배수이다.
확장 유클리드 알고리즘(Extended Euclidean Algorithm)
- 두 정수 a, b가 주어질 때, 다음을 만족하는 다른 두 정수 s와 t를 계산한다.
s * a + t * b = gcd(a,b)
즉, a와 b에 어떤 수를 더하고, 빼고 해서 결국 두 a,b 의 최대 공약수를 만족하는 s와 t를 찾는 것
초기 조건

진행

라고 되어있는데, 그냥 ri−1 즉, 나눈 나머지로 계산하면 편하다. (이때는 이여야함)
아래와 같이 표를 작성하면 편하다.

15s + 6t = 3을 만족시키는 s,t를 찾아보자.


위와 같이 ri == 0 이 된다면 종료!
구현 코드
# Euclidean Algorithm
import sys
a, b = map(int, sys.stdin.readline().split())
a_temp = a
b_temp = b
print(" ")
q, r, t, r = 0, 0, 0, 0
s_1, s_2 = 1, 0
t_1, t_2 = 0, 1
if a < b :
a, b = b, a # swap
while(True):
q = a // b
r = a - (q*b)
s = s_1 - (q * s_2)
t = t_1 - (q * t_2)
print(a ,'=', q, '*', b, '+', r)
if r == 0:
print("\ngcd = ", b)
print("s : ", s_2, ", t : ", t_2)
if b == 1:
print("relatively prime")
break
a = b
b = r
s_1 = s_2
s_2 = s
t_1 = t_2
t_2 = t
print(s_2 ,"*", a_temp, "+", t_2, "*", b_temp, "=", b)
모듈러 곱셈 역원
- 우선 곱셈의 역원이 존재한다는 것은 두 수가 서로소라는 것이다.
- 따라서, a * s = 1 (mod p)를 만족시키는 s를 찾을 수 있다는 의미이다.
- 여기서 s 는 a의 지수가 -1인 것을 의미한다.
- 그럼 아래의 식이 가능하다는 의미
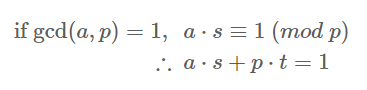
- 여기서 s는 음수가 될 수도 있음으로 양수인 곱셈 역원만 구하고 싶다면
- s_result <- (s_result + p) mod p 를 하면 된다.
반복을 이용한 모듈러 곰셈 역수
def find_mod_inv(a,m):
for x in range(1,m):
if((a%m)*(x%m) % m==1):
return x
raise Exception('The modular inverse does not exist.')
a = 13
m = 22
try:
res=find_mod_inv(a,m)
print("The required modular inverse is: "+ str(res))
except:
print('The modular inverse does not exist.')
pow() 내장 함수를 사용하여 모듈식 곱셈 역수 계산
a=38
m=97
res = pow(a, m-2, m)
print("The required modular inverse is: "+ str(res))- pow() 메서드를 사용하여 모듈로 곱셈 역을 계산하려면
- pow() 메서드의 첫 번째 매개변수는 모듈러 역함수를 찾을 숫자 이고
- 두 번째 매개변수는 모듈러에서 2를 뺀 순서
- 마지막 매개변수는 모듈러의 차수
- 파이썬 3.8 이상에선 두 번째 인수를 -1로 대체 가능
728x90
'ALGORITHM > 알고리즘 알아보기' 카테고리의 다른 글
| [Algorithm] Manacher's Algorithm (1) | 2023.01.21 |
|---|---|
| [Algorithm] 팰린드롬 판별 알고리즘 (0) | 2023.01.21 |
| [Algorithm] 플로이드-워셜 (0) | 2022.12.18 |
| [Algorithm] 최장 공통 부분 수열 (LCS) (0) | 2022.12.13 |
| [Algorithm] 유클리드 호제법 (최대 공약수, 최소 공배수) (0) | 2022.12.09 |
