728x90
앞에서는 배열을 선언하고 그 배열을 정렬하는 방법에 대해서 배웠다.
이번 글에서는 경우의 수를 이용하여 문제 해결을 하는 검색이라는 것에 대해서 배워보자.
완전 검색(Exaustive Search)
- 완전 검색 방법은 문제의 해법으로 생각할 수 있는 모든 경우의 수를 나열해보고 확인하는 기법
- Brute-force 혹은 generate-and-test 기법이라고도 불림
- 모든 경우의 수를 테스트한 후, 최종 해법을 도출
- 일반적으로 경우의 수가 상대적으로 작을 때 유용
- 특징
- 모든 경우의 수를 생성하고 테스트하기 때문에 수행 속도는 느리지만, 해답을 찾아내지 못할 확률이 작다.
- 평가 등에서 주어진 문제를 풀 때, 우선 완전 검색으로 접근하여 해답을 도출한 후, 성능 개선을 위해 다른 알고리즘을 사용하고 해답을 확인하는 것이 바람직
- 이를 기반으로 그리디 기법이나 동적 계획법을 이용해서 효율적인 알고리즘 찾을 수 있다.
완전 검색의 방법
- Brute Force기법 - 반복/조건문을 활용해 모두 테스트하는 방법
- 순열(Permutation) - n개의 원소 중 r개의 원소를 중복 허용 없이 나열하는 방법
- 재귀 호출
- 비트마스크 - 2진수 표현 기법을 활용하는 방법
- BFS, DFS를 활용하는 방법
즉, 조합적 문제들 (Combinatorial Probelms)와 연관된다.
Brute-force 탐색 (sequential search)
- 자료들의 리스트에서 키 값을 찾기 위해 첫 번째 자료부터 비교하면서 진행

글로 보면 이해가 잘 안될 수 있으니 Baby-gin 문제를 풀어보며 이해하자.
Baby-gin
- 0~9 사이의 숫자 카드에서 임의의 카드 6장을 뽑았을 때, 3장의 카드가 연속적인 번호를 갖는 경우를 run이라 하고, 3장의 카드가 동일한 번호를 갖는 경우를 triplet이라고 한다.
- 그리고, 6장의 카드가 run과 triplet로만 구성된 경우를 baby-gin으로 부른다.
1. 우선 고려할 수 있는 모든 경우의 수를 생성한다.
- 6개의 숫자로 만들 수 있는 모든 숫자 나열 (중복 포함)
- 예) 입력으로 [2,3,5,7,7,7]을 받았을 경우, 아래와 같이 순열 생성 가능

<모든 경우의 순열 나열>
2. 해답 테스트하기
- 앞의 3자리와 뒤의 3자리를 잘라, run와 triplet 여부를 테스트하고 최종적으로 baby-gin을 판단한다.

이런식으로 완전 검색을 통하여 풀어나가면 될 것이다.
그럼 모든 경우의 수의 순열은 어떻게 만들까?
순열(Permutation)
- 서로 다른 것들 중 몇 개을 뽑아서 한 줄로 나열하는 것
- 서로 다른 n개 중 r개를 택하는 순열은 아래와 같이 표현한다.
- nPr
- nPr = n * (n -1) * (n-2) * ... * (n-r+1)
- nPr = n! (Factorial)
- n! = n * (n -1) * (n-2) * ... * 2 * 1
- 예) 1, 2, 3을 포함하는 모든 순열 생성 함수

순열 생성 방법
1. 사전적 순서(Lexicographic-Order)
- [1 2 3] [1 3 2] [2 1 3] [2 3 1] [3 1 2] [3 2 1]
2. 최소 변경을 통한 방법(Minimum-exchange requirement)
- 각각의 순열들은 이전의 상태에서 단지 두 개의 요소들 교환을 통해 생성
- [1 2 3] [3 2 1] [2 3 1] [2 1 3] [3 1 2] [1 3 2]
- 1950년대의 교회 종소리 패턴과 유사하며 Johnson-Trotter 알고리즘이라고 한다.
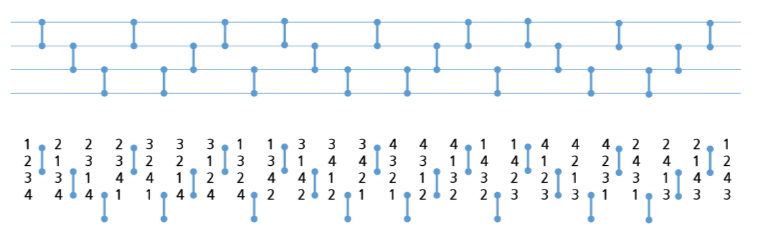
# 참고 - 1,2,3으로 구성된 순열
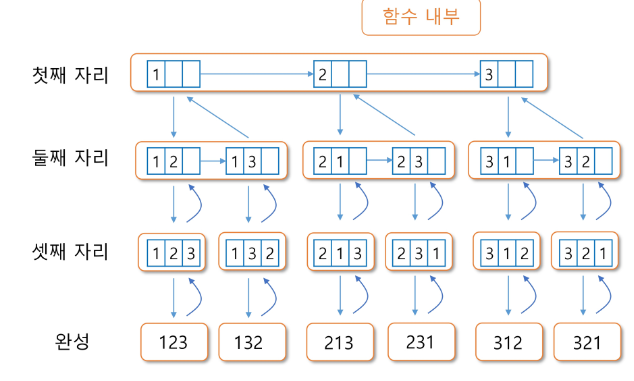
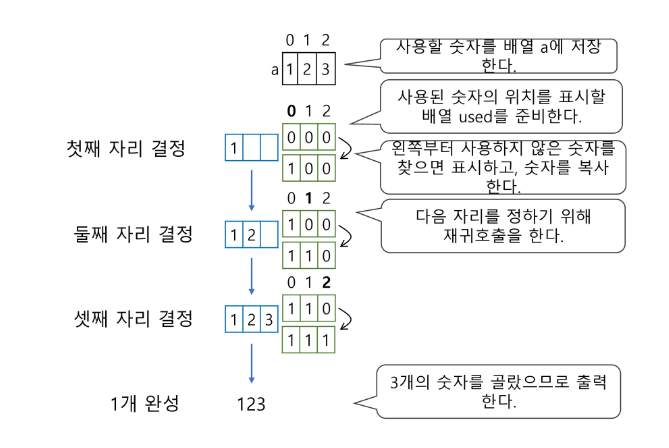

- 다수의 알고리즘 문제들은 순서화된 요소들의 집합에서 최선의 방법을 찾는 것과 관련
- 또한, N개의 요소들에 대해서 n!개의 순열들이 존재한다.
- n > 12인 경우, 시간 복잡도 폭발적으로 ↑
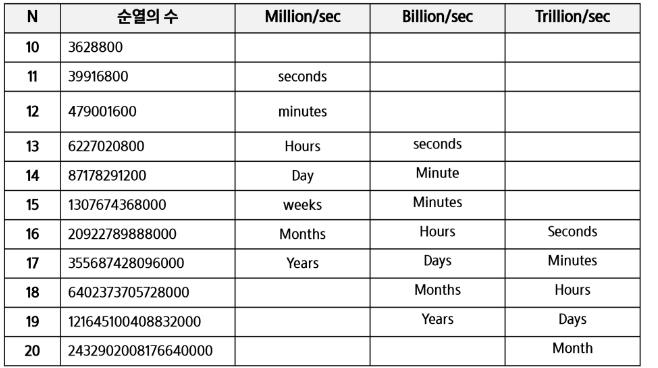
다음 시간에 greedy에 대해 배워보면서 더 쉽게 푸는 법을 배워보자.
728x90
'ALGORITHM > 알고리즘 알아보기' 카테고리의 다른 글
| [알고리즘] Memoization과 동적 프로그래밍 (0) | 2022.08.17 |
|---|---|
| 알고리즘 - 검색(Search) (0) | 2022.08.10 |
| 알고리즘 - 부분 집합 (0) | 2022.08.10 |
| 알고리즘 - 탐욕(Greedy) (0) | 2022.08.08 |
| ALGORITHM? (0) | 2022.08.08 |
