728x90
http://www.acmicpc.net/problem/10830
10830번: 행렬 제곱
크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
# 조건
- 크기가 N * N 인 행렬 A가 주어진다.
- 이 때, A의 B제곱을 구하는 프로그램을 작성
- 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다
입력
- 첫째 줄에 행렬의 크기 N과 B가 주어진다. (2 ≤ N ≤ 5, 1 ≤ B ≤ 100,000,000,000)
- 둘째 줄부터 N개의 줄에 행렬의 각 원소가 주어진다. 행렬의 각 원소는 1,000보다 작거나 같은 자연수 또는 0이다
# 접근 방법
- 우선 제곱해야될 횟수가 매우 클 수 있으므로 일일이 곱하면 시간 초과가 날 것이다.
- 따라서 분할 정복을 이용하여 구해준다.
- 우선 행렬의 곱셈은 아래와 같이 진행한다.
- 3중 반복문을 통하여 행렬의 곱셈을 구해주는 함수 작성
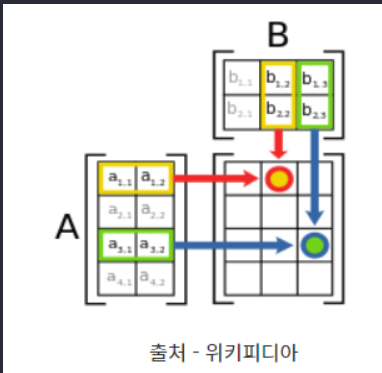
- 또한 분할 정복을 이용하여 제곱을 아래와 같이 나눠줄 수 있다.
- a^16 = a^8 * a^8
- a^8 = a^4 * a^4
- a^4 = a^2 * a^2
- a^2 = a * a
- a^4 = a^2 * a^2
- a^8 = a^4 * a^4
- 만약 지수가 홀수인 경우는 마지막에 a를 한 번 더 곱해주어야 한다.
import sys
sys.stdin = open('input.txt')
input = sys.stdin.readline
# 입력
N, B = map(int, input().split())
matrix = []
for _ in range(N):
matrix.append(list(map(int, input().split())))
# 행렬 곱셈
def mul_matrix(mat1, mat2):
res = [[0]*N for _ in range(N)]
for i in range(N):
for j in range(N):
for z in range(N):
# c11 = a11*b11 + a12*b21
res[i][j] += mat1[i][z] * mat2[z][j] % 1000
return res
# 분할정복
def power(a, b):
if b == 1: # b의 값이 1이 될 때까지 재귀
return a
else:
tmp = power(a, b // 2) # a^(b // 2)
if b % 2 == 0:
return mul_matrix(tmp, tmp) # b가 짝수인 경우
else:
return mul_matrix(mul_matrix(tmp, tmp), a) # b가 홀수인 경우
result = power(matrix, B)
# 출력
for row in result:
for col in row:
print(col % 1000, end=" ")
print()728x90
'ALGORITHM > 분할정복' 카테고리의 다른 글
| [백준 13172번] 파이썬 - ∑ (시그마) (1) | 2022.12.31 |
|---|---|
| [백준 11444번] 파이썬 - 피보나치 수 6 (0) | 2022.12.24 |
| [백준 1992번] 파이썬 - 쿼드트리 (0) | 2022.10.09 |
| [백준 2630번] 파이썬 - 색종이 만들기 (1) | 2022.10.08 |
| [백준 1780번] 파이썬 - 종이의 개수 (0) | 2022.10.06 |
